早教吧作业答案频道 -->数学-->
平面直角坐标系中有函数y1、y2、y3,y1=ax2+bx+c(a≠0),y2=-x2+2x,y3=kx+b(k≠0),y1的图象向右平移2个单位,再向上平移1个单位后与y2的图象重合,y3经过y1与y轴的交点以及y2的顶点.(1)求y
题目详情
平面直角坐标系中有函数y1、y2、y3,y1=ax2+bx+c(a≠0),y2=-x2+2x,y3=kx+b(k≠0),y1的图象向右平移2个单位,再向上平移1个单位后与y2的图象重合,y3经过y1与y轴的交点以及y2的顶点.
(1)求y1和y3的表达式;
(2)当x≥0时,试比较y2与y3的大小;
(3)当x<m时,y1,y2,y3均随着x的增大而增大,求实数m的最大值.
(1)求y1和y3的表达式;
(2)当x≥0时,试比较y2与y3的大小;
(3)当x<m时,y1,y2,y3均随着x的增大而增大,求实数m的最大值.
▼优质解答
答案和解析
(1)∵y1向右平移2个单位,向上平移1个单位得到y2,
∴y2向左平移2个单位,向下平移1个单位得到y1,
∵y2=-x2+2x,
∴y1=-(x+2)2+2(x+2)-1,
∴y1的表达式为y1=-x2-2x-1,
∴y1与y轴的交点为(0,-1).
∵y2=-x2+2x=-(x-1)2+1,
∴y2的顶点坐标为(1,1).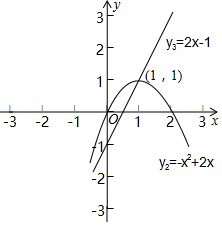
∵y3经过(0,-1)、(1,1),
∴
,解得:
,
∴y3的表达式为y3=2x-1.
(2)依照题意,画出函数y2、y3的图象,如图所示.
观察函数图象,可得:
当0≤x<1时,y2>y3;
当x=1时,y2=y3;
当x>1时,y2<y3.
(3)∵y1=-x2-2x-1=-(x+1)2,y2=-(x-1)2+1,y3=2x-1,
∴y1在x≤-1时随x的增大而增大,y2在x≤1时随x的增大而增大,y3一直都随x的增大而增大,
∴m≤-1时,y1,y2,y3均随着x的增大而增大,
∴m的最大值为-1.
∴y2向左平移2个单位,向下平移1个单位得到y1,
∵y2=-x2+2x,
∴y1=-(x+2)2+2(x+2)-1,
∴y1的表达式为y1=-x2-2x-1,
∴y1与y轴的交点为(0,-1).
∵y2=-x2+2x=-(x-1)2+1,
∴y2的顶点坐标为(1,1).
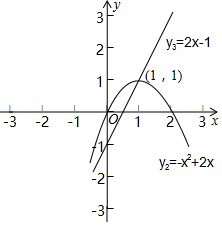
∵y3经过(0,-1)、(1,1),
∴
|
|
∴y3的表达式为y3=2x-1.
(2)依照题意,画出函数y2、y3的图象,如图所示.
观察函数图象,可得:
当0≤x<1时,y2>y3;
当x=1时,y2=y3;
当x>1时,y2<y3.
(3)∵y1=-x2-2x-1=-(x+1)2,y2=-(x-1)2+1,y3=2x-1,
∴y1在x≤-1时随x的增大而增大,y2在x≤1时随x的增大而增大,y3一直都随x的增大而增大,
∴m≤-1时,y1,y2,y3均随着x的增大而增大,
∴m的最大值为-1.
看了 平面直角坐标系中有函数y1、...的网友还看了以下:
已知三角形OAB的顶点坐标为O(0,0),A(2,9),B(6,-3),点p的横坐标为14,且向量 2020-06-02 …
四边形的四个顶点必须按顺时针或逆时针方向?还是没有要求呢如题1:如果已知平行四边形ABCD中A(2 2020-06-06 …
已知二次函数y=x²-x+m(1)判断该函数图象的开口方向并求对称轴及顶点坐标(2)当m取何值已知 2020-06-14 …
梁顶相对标高高差在钢筋抽样里起点顶标高那栏应该选层顶标高还是洞口顶标高加连梁高度啊比如,梁顶标高差 2020-07-01 …
二次函数y=ax^2+x+a^2-1的图像可能是A函数开口向上,顶点坐标在第4象限,函数过原点B函 2020-07-21 …
如图,矩形ABCD四个顶点分别是A(-3,2),B(-3,-2),C(3,-2),D(3,2),将 2020-07-31 …
平面直角坐标1.在直角坐标系中,某三角形纵向拉长2倍,又向右平移了3个单位长度,所得的三角形的三个 2020-08-01 …
∵抛物线的开口向上,顶点纵坐标为-3,∴a>0.-b^2/4a=-3即b^2=1∵抛物线的开口向上 2020-08-01 …
一,求下列二次函数,图像的开口方向,顶点坐标和对称轴(不用配方)1、y=2x^2-8x+12、y= 2020-08-01 …
空间中两个过原点向量,已知两向量夹角,知道一个向量顶点坐标.怎么求出另一向量的定点坐标?模长也是已 2020-08-02 …