早教吧作业答案频道 -->数学-->
如图1,在Rt△ABC中,∠ACB=90°,D为CB上一点,且满足CD=CA,连接AD.过点C作CE⊥AB于点E.(1)若AB=10,BD=2,求CE的长;(2)如图2,若点F是线段CE延长线上一点,连接FD,若∠F=30°,求证:CF=AE+
题目详情
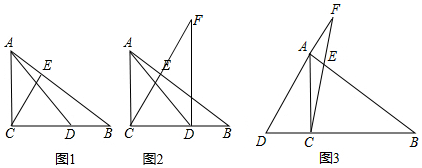
如图1,在Rt△ABC中,∠ACB=90°,D为CB上一点,且满足CD=CA,连接AD.过点C作CE⊥AB于点E.
(1)若AB=10,BD=2,求CE的长;
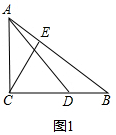
(2)如图2,若点F是线段CE延长线上一点,连接FD,若∠F=30°,求证:CF=AE+
DF;
(3)如图3,设D为BC延长线上一点,其它条件不变,直线CE与直线AD交于点F,若∠F=30°,请直接写出线段CF,AE,DF之间的关系,不需要说明理由.
(1)若AB=10,BD=2,求CE的长;
(2)如图2,若点F是线段CE延长线上一点,连接FD,若∠F=30°,求证:CF=AE+
| ||
| 2 |
(3)如图3,设D为BC延长线上一点,其它条件不变,直线CE与直线AD交于点F,若∠F=30°,请直接写出线段CF,AE,DF之间的关系,不需要说明理由.

▼优质解答
答案和解析
(1) 如图1中,设AC=CD=x.
在Rt△ACB中,AB=10,AC=x,BC=CD+BD=x+2,
∵AB2=AC2+BC2,
∴102=x2+(x+2)2,
解得x=6或-8(舍弃),
∴AC=6.
∵
•AC•BC=
•AB•CE,
∴CE=
=
.
(2)证明:如图2中,作DH⊥CF于H.
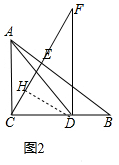
∵∠ACD=∠AEC=∠DHC=90°,
∴∠ACE+∠CAE=90°,∵∠ACE+∠BCE=90°,
∴∠CAE=∠DCH,
在△ACE和∠CDH中,
,
∴△ACE≌△CDH,
∴AE=CH,
在Rt△DHF中,∵∠DHF=90°,∠F=30°,
∴HF=DF•cos30°=
DF,
∴CF=CH+FH=AE+
DF.
(3) 结论:CF=
DF-AE.
理由:如图3中,作DH⊥FC于H.
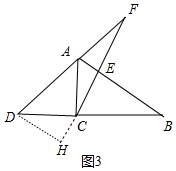
同法可证△DCH≌△CAE,
∴AE=CH,
在Rt△DHF中,∵∠DHF=90°,∠F=30°,
∴HF=DF•cos30°=
DF,
∴CF=FH-CH=
DF-AE.

在Rt△ACB中,AB=10,AC=x,BC=CD+BD=x+2,
∵AB2=AC2+BC2,
∴102=x2+(x+2)2,
解得x=6或-8(舍弃),
∴AC=6.
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
| 6×8 |
| 10 |
| 24 |
| 5 |
(2)证明:如图2中,作DH⊥CF于H.

∵∠ACD=∠AEC=∠DHC=90°,
∴∠ACE+∠CAE=90°,∵∠ACE+∠BCE=90°,
∴∠CAE=∠DCH,
在△ACE和∠CDH中,
|
∴△ACE≌△CDH,
∴AE=CH,
在Rt△DHF中,∵∠DHF=90°,∠F=30°,
∴HF=DF•cos30°=
| ||
| 2 |
∴CF=CH+FH=AE+
| ||
| 2 |
(3) 结论:CF=
| ||
| 2 |
理由:如图3中,作DH⊥FC于H.

同法可证△DCH≌△CAE,
∴AE=CH,
在Rt△DHF中,∵∠DHF=90°,∠F=30°,
∴HF=DF•cos30°=
| ||
| 2 |
∴CF=FH-CH=
| ||
| 2 |
看了 如图1,在Rt△ABC中,∠...的网友还看了以下:
已知△ABC为等边三角形,点P在射线BA上,点Q在直线BC上PQ=PC,1.当点P在线段BA的延长线 2020-03-30 …
已知两根木条,一根长ab=60cm一根长cd=100cm)将它们的一端重合,(a与c重合)放在同一 2020-05-23 …
一、注意审题,仔细填空:35%(2+3+3+2+2+2+2+2+1+3+9+4)1、连接圆心和圆上 2020-07-11 …
如图,已知数轴上点A、B、C所对应的数a、b、c都不为0,且C是AB的中点.如果|a+b|-|a- 2020-07-20 …
如图,若数轴上的点A,B,C,D表示数-2,1,2,3,则表示4-7的点P应在线段()A.线段AB 2020-07-21 …
画一条线段的垂线,垂足一定在()A.线段上B.线段的端点C.线段的延长线上D.线段所在的直线上 2020-07-21 …
四边形ABCD是直角梯形上底DC=3下底AB=9线段DE,EF把梯形分成面积相等三块,四边形ABC 2020-07-30 …
(2012•内江市0区模拟)8图,直角梯形纸片9BCD,9D⊥9B,9D=CD=图,点E、F分别在线 2020-11-12 …
数学找规律题线段AB上的点数包括端点与线段的总数有如下关系:如果线段上有2个点时,可以确定1条线段; 2020-11-27 …
已知线段AB=5cm1.在线段AB上画线段BC=3厘米,并求线段AC的长2.在直线AB上画线段BC= 2020-12-23 …