早教吧作业答案频道 -->数学-->
在等腰直角三角形ABC中,∠ACB=90°,AC=3,点P为边BC的三等分点,连接AP,则AP的长为.
题目详情
在等腰直角三角形ABC中,∠ACB=90°,AC=3,点P为边BC的三等分点,连接AP,则AP的长为___.
▼优质解答
答案和解析
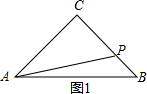 ①如图1,∵∠ACB=90°,AC=BC=3,
①如图1,∵∠ACB=90°,AC=BC=3,
∵PB=
BC=1,
∴CP=2,
∴AP=
=
,
②如图2,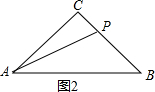 ∵∠ACB=90°,AC=BC=3,
∵∠ACB=90°,AC=BC=3,
∵PC=
BC=1,
∴AP=
=
,
综上所述:AP的长为
或
,
故答案为:
或
.
 ①如图1,∵∠ACB=90°,AC=BC=3,
①如图1,∵∠ACB=90°,AC=BC=3,∵PB=
| 1 |
| 3 |
∴CP=2,
∴AP=
| AC2+PC2 |
| 13 |
②如图2,
 ∵∠ACB=90°,AC=BC=3,
∵∠ACB=90°,AC=BC=3,∵PC=
| 1 |
| 3 |
∴AP=
| AC2+PC2 |
| 10 |
综上所述:AP的长为
| 13 |
| 10 |
故答案为:
| 13 |
| 10 |
看了 在等腰直角三角形ABC中,∠...的网友还看了以下:
在△ABC中AB=AC=5BC=6点P在BC上(不与B.C重合)作PE⊥AB垂足为E、作PF⊥BC 2020-05-14 …
点P是矩形ABCD的边AD上的一个动点,矩形的两条边长AB、BC分别为8和15,求点P到矩形的两条 2020-05-20 …
如图,在角ABC中,AB=AC,点P为角角ABC内一点,且角ACP=角CBP,角A=50度,则角B 2020-06-27 …
已知a,b,c是三角形ABC的三边长,(a-5)^2+|b-12|+c^2-26c+169=0,则 2020-07-18 …
椭圆,双曲线中的三角形面积问题已知椭圆焦点F1,F2.和椭圆上一点P,三角形P,F1,F2的面积是 2020-07-26 …
点P三角形ABC所在平面外一点,A',B',C'分别是三角形PBC,三角形PCA,三角形PAB的重 2020-07-30 …
已知△ABC中,∠ACB=90°,AC=3,BC=4,P是AB上中点,Q是BC上动点且不与BC重合 2020-08-03 …
1.如图1,已知角ABC=45度,P为角ABC内部一点,PE//AB,PF//BC,分别交BC.BA 2020-11-03 …
△ABC为等腰三角形,AB=AC=a,P点是底边BC上的一个动点,PD‖AC,PE‖AB.(1)用a 2020-12-25 …
.假定p是具有int**类型的指针变量,则给p赋值的正确语句为(B)。A.p=newint;B.p= 2020-12-31 …