早教吧作业答案频道 -->数学-->
如图,已知椭圆x2a2+y2b2=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.(1)若∠F1AB=90°,求椭圆的离心率;(2)若椭圆的焦距为2,且AF2=2F2B,
题目详情
如图,已知椭圆
+
=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
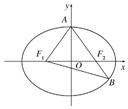
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若椭圆的焦距为2,且
=2
,求椭圆的方程.
| x2 |
| a2 |
| y2 |
| b2 |

(1)若∠F1AB=90°,求椭圆的离心率;
(2)若椭圆的焦距为2,且
| AF2 |
| F2B |
▼优质解答
答案和解析
(1)若∠F1AB=90°,则△AOF2为等腰直角三角形.则|OA|=|OF2|,即b=c.
∴a=
=
c,
椭圆的离心率e=
=
;
(2)由题知2c=2,c=1,则A(0,b),F2(1,0),设B(x,y),
由
=2
,即(1,-b)=2(x-1,y),
∴
,解得x=
,y=-
.
代入椭圆
+
=1,即
+
=1解得a2=3.b2=a2-c2=2,
∴椭圆方程为
+
=1.
∴a=
| b2+c2 |
| 2 |
椭圆的离心率e=
| c |
| a |
| ||
| 2 |
(2)由题知2c=2,c=1,则A(0,b),F2(1,0),设B(x,y),
由
| AF2 |
| F2B |
∴
|
| 3 |
| 2 |
| b |
| 2 |
代入椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| 9 |
| 4a2 |
| 1 |
| 4 |
∴椭圆方程为
| x2 |
| 3 |
| y2 |
| 2 |
看了 如图,已知椭圆x2a2+y2...的网友还看了以下:
国标规定,单个圆柱齿轮的( )用粗实线绘制。A.齿顶圆和齿顶线B.分度圆和分度线C.齿根圆和齿根线D 2020-06-07 …
已知椭圆C:x2a2+y2b2=1(a>b>0)经过点(1,32),离心率为32.(Ⅰ)求椭圆C的 2020-06-21 …
与双曲线-y2=1有公共焦点,且离心率为.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x 2020-07-21 …
当双曲线C不是等轴双曲线时,我们把以C的实轴、虚轴的端点作为顶点的椭圆称为双曲线C的“伴生椭圆”. 2020-07-30 …
已知椭圆C:x2a2+y2b2=1(a>b>0)的焦距为2,其两个焦点与短轴的一个顶点是正三角形的 2020-07-31 …
知椭圆E:x2a2+y2b2=1(a>b>0)的两个焦点与短轴的一个端点是等边三角形的三个顶点.且 2020-07-31 …
设双曲线的左、右焦点为F1,F2,左、右顶点为M,N,若△PF1F2的顶点P在双曲线上,则△PF1 2020-08-01 …
巳知椭圆C:x2a2+y2b2=1与双曲线x22-y2=1有公共焦点,且离心率为32.A、B分别是 2020-08-02 …
如图甲,固定在光滑水平面上的正三角形金属线框,匝数n=20,总电阻R=2.5Ω,边长L=0.3m.处 2020-11-11 …
如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则 2020-12-05 …