早教吧作业答案频道 -->数学-->
已知平行四边形ABCD的面积为60cm2,点P是其内部一点,连接PA,PB,PC,PD,将平行四边形分成四个三角形,其面积分别记为如图所示的S1、S2、S3、S4.如果过P点分别做上述四个三角形的高,你
题目详情
已知平行四边形ABCD的面积为60cm2,点P是其内部一点,连接PA,PB,PC,PD,将平行四边形分成四个三角形,其面积分别记为如图所示的S1、S2、S3、S4.如果过P点分别做上述四个三角形的高,你会发现S1、S2、S3、S4满足S1+S3=S2+S4,请应用这个结论解决下列问题:
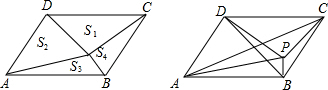
(1)若S2=2S1,S3=3S4,求S1+S2的值.
(2)在(1)的条件下,连接AC、BD,求三角形PBD与三角形PAC的面积和.

(1)若S2=2S1,S3=3S4,求S1+S2的值.
(2)在(1)的条件下,连接AC、BD,求三角形PBD与三角形PAC的面积和.
▼优质解答
答案和解析
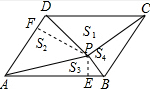 (1)如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
(1)如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AD与BC的距离,∴S2+S4=
S四边形ABCD=30,
同理可得出S1+S3=
S四边形ABCD=30,
∴S2=
S四边形ABCD-S4=30-S4,
∵S2=2S1,S3=3S4,
∴S1+S3=S1+3S4=S1+3(30-S2)=S1+3(30-2S1)=30,
∴S1=12,
∴S2=24,
∴S1+S2=36;
(2)由(1)知S1=12,S2=24,
∴S3=30-12=18,S4=30-24=6,
∴S△PBD+S△PAC
=S△BDC-S1-S4+S△ABC-S3-S4
=
S四边形ABCD-S1-S4+
四边形ABCD-S3-S4
=18.
 (1)如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
(1)如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AD与BC的距离,∴S2+S4=
| 1 |
| 2 |
同理可得出S1+S3=
| 1 |
| 2 |
∴S2=
| 1 |
| 2 |
∵S2=2S1,S3=3S4,
∴S1+S3=S1+3S4=S1+3(30-S2)=S1+3(30-2S1)=30,
∴S1=12,
∴S2=24,
∴S1+S2=36;
(2)由(1)知S1=12,S2=24,
∴S3=30-12=18,S4=30-24=6,
∴S△PBD+S△PAC
=S△BDC-S1-S4+S△ABC-S3-S4
=
| 1 |
| 2 |
| 1 |
| 2 |
=18.
看了 已知平行四边形ABCD的面积...的网友还看了以下:
已知等边三角形ABC内接于⊙O,P为⊙O上异于A、B、C的动点.当点P为弦BC所对的劣弧上一点时( 2020-06-23 …
一弹簧秤的称盘质量M1=1.5Kg,盘内放一物体P,P的质量M2=10.5Kg.弹簧质量不计.其劲 2020-06-30 …
如图所示,在与直流电源相接的平行板电容器内部,有一个小带电体P正好处于受力平衡状态.问:(1)当将 2020-06-30 …
所有、有的;p,非p已知P代表:有的A不是B,那么非P如何表示?如果P代表:有的A是B,那么非P如 2020-07-01 …
(2014•市中区一模)已知在Rt△ABC中,∠ABC=90°,∠A=30°,点P在BC上,且∠M 2020-07-27 …
八年级数学几何在直角三角形ABC中,角C=90°,AC=BC,M是AB的中点,P是AB上任意一点, 2020-07-30 …
求贝叶斯两种公式形式的互相推导贝叶斯定理公式:P(A|B)=P(B|A)*P(A)/P(B)如上公 2020-07-30 …
如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.(1)试证明:无 2020-11-04 …
如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.(1)试证明:无 2020-11-04 …
求你们了!真的不会!谁会,大大地有赏设f(x)=x^2+px+q,g(x)=x^2+qx+p,p、q 2020-12-31 …