如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BC•AD=2AE2；④S△ABC=4S△ADF．其中正确的有（）A.1个B.2

Question

如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BC•AD=

√(2)AE²；④S_△ABC=4S_△ADF．其中正确的有（　　）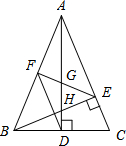

A. 1个

B. 2 个

C. 3 个

D. 4个

Answer 1

∵在△ABC中，AD和BE是高，
∴∠ADB=∠AEB=∠CEB=90°，
∵点F是AB的中点，
∴FD=(1)/(2)AB，
∵∠ABE=45°，
∴△ABE是等腰直角三角形，
∴AE=BE，
∵点F是AB的中点，
∴FE=(1)/(2)AB，
∴FD=FE，①正确；
∵∠CBE=∠BAD，∠CBE+∠C=90°，∠BAD+∠ABC=90°，
∴∠ABC=∠C，
∴AB=AC，
∵AD⊥BC，
∴BC=2CD，∠BAD=∠CAD=∠CBE，
在△AEH和△BEC中，

∠AEH=∠CEB

AE=BE

∠EAH=∠CBE

，
∴△AEH≌△BEC（ASA），
∴AH=BC=2CD，②正确；
∵∠BAD=∠CBE，∠ADB=∠CEB，
∴△ABD～△BCE，
∴(BC)/(AB)=(BE)/(AD)，即BC•AD=AB•BE，
∵√(2)AE²=AB•AE=AB•BE，BC•AD=AC•BE=AB•BE，
∴BC•AD=√(2)AE²；③正确；
∵F是AB的中点，BD=CD，∴
S_△ABC=2S_△ABD=4S_△ADF．④正确；
故选：D．