早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.(1)求点A,B的坐标;(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与
题目详情
在平面直角坐标系xOy中,抛物线y=mx2-2mx+2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
(1)求点A,B的坐标;
(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与线段CD有两个公共点,结合函数的图象,求m的取值范围.
(1)求点A,B的坐标;
(2)点C,D在x轴上(点C在点D的左侧),且与点B的距离都为2,若该抛物线与线段CD有两个公共点,结合函数的图象,求m的取值范围.
▼优质解答
答案和解析
(1)由题意,当x=0时,y=2.
∴A(0,2).
∵y=mx2-2mx+2=m(x-1)2+2-m,
∴对称轴为直线x=1.
∴B(1,0).
(2)由题意,C(-1,0),D(3,0).
①当m>0时,
结合函数图象可知,满足题意的抛物线的顶点须在x轴下方,
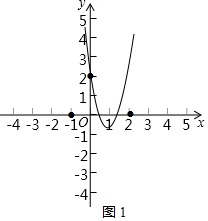
即2-m<0.
∴m>2.
②当m<0时,
过C(-1,0)的抛物线的顶点为E(1,
).
结合函数图象可知,满足条件的抛物线的顶点须在点E上方或与点E重合,
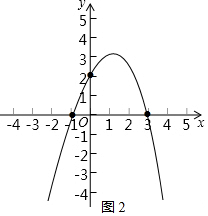
即2-m≥
.
∴m≤-
.
综上所述,m的取值范围为m>2或m≤-
.
∴A(0,2).
∵y=mx2-2mx+2=m(x-1)2+2-m,
∴对称轴为直线x=1.
∴B(1,0).
(2)由题意,C(-1,0),D(3,0).
①当m>0时,
结合函数图象可知,满足题意的抛物线的顶点须在x轴下方,

即2-m<0.
∴m>2.
②当m<0时,
过C(-1,0)的抛物线的顶点为E(1,
| 8 |
| 3 |
结合函数图象可知,满足条件的抛物线的顶点须在点E上方或与点E重合,

即2-m≥
| 8 |
| 3 |
∴m≤-
| 2 |
| 3 |
综上所述,m的取值范围为m>2或m≤-
| 2 |
| 3 |
看了 在平面直角坐标系xOy中,抛...的网友还看了以下:
在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.(1)如图①,当点O在AC上时 2020-05-13 …
(几何证明选讲)如图,半径是33的⊙O中,AB是直径,MN是过点A的⊙O的切线,AC,BD相交于点 2020-05-14 …
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.(1)求证 2020-05-16 …
如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A 2020-05-17 …
如图所示,已知A,B是圆O上的两点,∠AOB=120°,C是弧AB的中点,若圆O的半径为4㎝,求四 2020-05-19 …
如图,AB是⊙O的直径,点P是⊙O上的动点(P与A,B不重合),连接AP,PB,过点O分别作OE⊥ 2020-05-23 …
已知点P和○O(尺规作图)(1)若点P在○O内求做○O的弦AB使它以点P为中点(2)若点P在○O上 2020-06-06 …
直线4x+3y=12于坐标轴交与AB两点,圆o的圆心在原点上与线段AB有两个交点,直线4x+3y= 2020-06-10 …
已知,Rt△ABC中,∠C=90°,AC=4,BC=3.以AC上一点O为圆心的⊙O与BC相切于点C 2020-06-15 …
图1,过点O上一点P作两条弦PAPB,若PA=PB则PO平分∠APB,为什么.如图2,若P在圆内图 2020-06-17 …