(本小题满分14分)已知椭圆的中心在坐标原点,两个焦点分别为,,点在椭圆上,过点的直线与抛物线交于两点,抛物线在点处的切线分别为,且与交于点.(1)求椭圆的方程;(2)
(本小题满分14分)
已知椭圆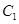 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为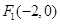 ,
,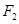
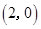 ,点
,点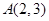 在椭圆
在椭圆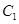 上,过点
上,过点 的直线
的直线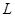 与抛物线
与抛物线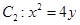 交于
交于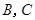 两点,抛物线
两点,抛物线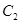 在点
在点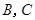 处的切线分别为
处的切线分别为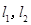 ,且
,且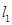 与
与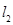 交于点
交于点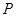 .
.
(1) 求椭圆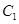 的方程;
的方程;
(2) 是否存在满足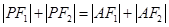 的点
的点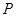 ? 若存在,指出这样的点
? 若存在,指出这样的点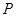 有几个(不必求出点
有几个(不必求出点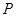 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
急求椭球的方程已知椭球两焦点分别为(100,2000,2000)和(1,5,5),且椭球上的点到两 2020-05-15 …
关于过已知两点求椭圆方程问题按照老师所讲,已知两点求过两点椭圆方程时,需分类讨论:椭圆在x轴上时 2020-05-16 …
已知椭圆的中心在原点,两焦点F1,F2在x轴上,且过点A(-4,3).(1)若F1A⊥F2A,求椭 2020-05-17 …
已知F1,F2分别是椭圆(a>b>0)的左、右焦点,半焦距为c,直线x=-与x轴的交点为N,满足, 2020-07-20 …
(本小题满分14分)已知椭圆的中心在坐标原点,两个焦点分别为,,点在椭圆上,过点的直线与抛物线交于 2020-07-20 …
设p(x0,y0)是椭圆x^2/a^2+y^2/b^2=1(a>b>0)上一定点,过P点做两条直线 2020-07-30 …
(本小题满分14分)已知椭圆的离心率为,椭圆短轴的一个端点与两个焦点构成的三角形的面积为.(Ⅰ)求 2020-07-31 …
已知椭圆的中心在原点,焦点在x轴上,左右焦点分别为f1,f2,|f1f2|=2,且椭圆的一个顶点与两 2020-10-30 …
我没学过数学应付考试关于椭圆长轴椭圆的焦距是6,椭圆上一点到两个焦点之和是10,写出这个椭圆的标准方 2021-01-09 …
求满足下列条件的椭圆的标准方程,并画出草图.(1)椭圆的一个焦点为(-4,0),且与x轴的交点是(5 2021-01-15 …