早教吧作业答案频道 -->数学-->
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.已知:如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F
题目详情
证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知:如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴___=___(___).
同理可得,PB=___.
∴___=___(等量代换).
∴___(到一条线段两个端点距离相等的点,在这条线段的___)
∴AB、BC、AC的垂直平分线相交于点P,且___.
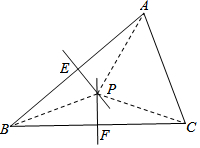
已知:如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴___=___(___).
同理可得,PB=___.
∴___=___(等量代换).
∴___(到一条线段两个端点距离相等的点,在这条线段的___)
∴AB、BC、AC的垂直平分线相交于点P,且___.

▼优质解答
答案和解析
 证明:∵点P是AB边垂直平线上的一点,
证明:∵点P是AB边垂直平线上的一点,
∴PB=PA (垂直平分线上任意一点,到线段两端点的距离相等).
同理可得,PB=PC.
∴PA=PC(等量代换).
∴点P是AC边垂直平线上的一点(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
∴AB、BC、AC的垂直平分线相交于点P,且PA=PB=PC.
故答案为:PB;PA;垂直平分线上任意一点,到线段两端点的距离相等;PC;PA;PC;点P在AC的垂直平分线上,垂直平分线上;PA=PB=PC.
 证明:∵点P是AB边垂直平线上的一点,
证明:∵点P是AB边垂直平线上的一点,∴PB=PA (垂直平分线上任意一点,到线段两端点的距离相等).
同理可得,PB=PC.
∴PA=PC(等量代换).
∴点P是AC边垂直平线上的一点(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
∴AB、BC、AC的垂直平分线相交于点P,且PA=PB=PC.
故答案为:PB;PA;垂直平分线上任意一点,到线段两端点的距离相等;PC;PA;PC;点P在AC的垂直平分线上,垂直平分线上;PA=PB=PC.
看了 证明定理:三角形三条边的垂直...的网友还看了以下:
社交礼仪作业、1.、简述敬人三A理论2、双向沟通理论在服务工作中有哪些重要作用?3、谈谈你所了解到 2020-06-05 …
对于函数f(x),若对于任意的a,b,c∈R,f(a),f(b),f(c)为某一三角形的三边长,则 2020-06-08 …
保三角函数一个函数f(x),图过对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内, 2020-06-20 …
有没有高手教下保三角函数具体怎么解!一个函数f(x),图过对任意一个三角形,只要它的三边长a,b, 2020-06-20 …
f(x)在[0,1]上有三阶导数,f(1)=0,设F(x)=x^3f(x),证(0,1)内一点A, 2020-06-22 …
已知函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a 2020-07-11 …
判断以下对应是否为从集合A到B的映射,并说明理由.(1)A={平面内的圆},B={平面内的三角形} 2020-07-30 …
对于一个函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f( 2020-11-11 …
(文)一个函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f 2020-11-20 …
若函数f(x)在区间A上,对∀a,b,c∈A,f(a),f(b),f(c)为一个三角形的三边长,则称 2020-11-20 …