如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为()A.44°B.66°C.96°D.92°
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )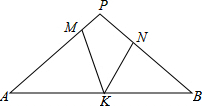
A. 44°
B. 66°
C. 96°
D. 92°
∴∠A=∠B,
在△AMK和△BKN中,
|
∴△AMK≌△BKN,
∴∠AMK=∠BKN,
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,
∴∠A=∠MKN=42°,
∴∠P=180°-∠A-∠B=96°,
故选:C.
四面体pabc中,pa垂直于bc,e,f分别为pc.ab的中点,若ef与pa,bc成的角分别为角1 2020-04-12 …
已知A、B、P是双曲线x^2/a^2-y^2/b^2=1(a>0,b>0)上不同的三点,且A、B两 2020-05-16 …
巳知点A、B、C的坐标分别为(0,1,0),(-1,0,1),(2,1,1),若向量PA⊥向量AB 2020-06-14 …
已知P是△ABC内任意一点。(1)试判断PB+PC<BA+AC是否成立?若成立,请说明理由。(2) 2020-06-15 …
2:若a,b满足a+2b=1,则直线ax+3y+b=0必过定点()3:点(4.0)关于直线5x+4 2020-07-18 …
如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB 2020-07-21 …
设A,B是x轴上的两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为x-y+1=0, 2020-07-21 …
(2014•东城区二模)在棱长为1的正方体ABCD-A1B1C1D1中,点P是正方体棱上一点(不包 2020-07-30 …
已知P是△ABC所在平面上一点,若向量PA点乘向量PB=向量PB点乘向量PC=向量PC点乘向量PA 2020-07-30 …
数学选择题P是△ABC所在平面上的一点,若向量PA·PB=PB·PC=PC·PA,则P是的什么心? 2020-07-30 …