如图，点A是双曲线y=8x在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运

Question

如图，点A是双曲线y=

(8)/(x)在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为（　　）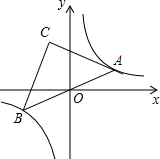

A. y=

(8)/(x)

B. y=

(16)/(x)

C. y=-

(16)/(x)

D. y=-

(8)/(x)

Answer 1

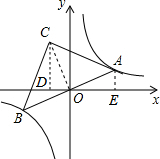如图，连结OC，作CD⊥x轴于D，AE⊥x轴于E，
∵A点、B点是正比例函数图象与双曲线y=(8)/(x)的交点，
∴点A与点B关于原点对称，
∴OA=OB，
∵△ABC为等腰直角三角形，
∴OC=OA，OC⊥OA，
∴∠DOC+∠AOE=90°，
∵∠DOC+∠DCO=90°，
∴∠DCO=∠AOE，
∵在△COD和△OAE中，

∠CDO=∠OEA

∠DCO=∠EOA

CO=OA

，
∴△COD≌△OAE（AAS），
设A点坐标为（a，(8)/(a)），则OD=AE=(8)/(a)，CD=OE=a，
∴C点坐标为（-(8)/(a)，a），
∵-(8)/(a)•a=-8，
∴点C在反比例函数y=-(8)/(x)图象上．
故选（D）