早教吧作业答案频道 -->数学-->
(1)如图1,已知△ABC,以AB、AC为边分别向外作正方形ABFD和正方形ACGE,连结BE、CD,猜想BE与CD有什么数量关系?并说明理由;(2)请模仿正方形情景下构造全等三角形的思路,利用构造全
题目详情
(1)如图1,已知△ABC,以AB、AC为边分别向外作正方形ABFD和正方形ACGE,连结BE、CD,猜想BE与CD有什么数量关系?并说明理由;
(2)请模仿正方形情景下构造全等三角形的思路,利用构造全等三角形完成下题:如图2,要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长(结果保留根号).
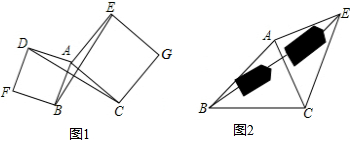
(2)请模仿正方形情景下构造全等三角形的思路,利用构造全等三角形完成下题:如图2,要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长(结果保留根号).

▼优质解答
答案和解析
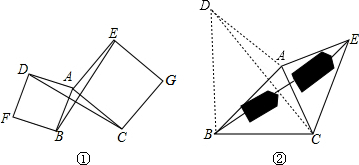 (1)CD=BE.
(1)CD=BE.
理由:如图①∵四边形ABFD和四边形ACGE都是正方形,
∴AD=AB,AC=AE,∠DAB=∠CAE=90°,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE中,
,
∴△ADC≌△ABE(SAS),
∴CD=BE;
(2)如图②,在AB的外侧作AD⊥AB,使AD=AB,连结CD,BD,
∴∠DAB=90°,
∴∠ABD=∠ADB=45°.
∵∠ABC=45°,
∴∠ABD+∠ABC=45°+45°=90°,
即∠DBC=90°.
∴∠CAE=90°,
∴∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE.
在△ADC和△ABE中
,
∴△ADC≌△ABE(SAS),
∴CD=BE.
∵AB=100m,在直角△ABD中,由勾股定理,得
BD=100
.
∴CD=
=100
,
∴BE=CD=100
,
答:BE的长为100
米.
 (1)CD=BE.
(1)CD=BE.理由:如图①∵四边形ABFD和四边形ACGE都是正方形,
∴AD=AB,AC=AE,∠DAB=∠CAE=90°,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE中,
|
∴△ADC≌△ABE(SAS),
∴CD=BE;
(2)如图②,在AB的外侧作AD⊥AB,使AD=AB,连结CD,BD,
∴∠DAB=90°,
∴∠ABD=∠ADB=45°.
∵∠ABC=45°,
∴∠ABD+∠ABC=45°+45°=90°,
即∠DBC=90°.
∴∠CAE=90°,
∴∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE.
在△ADC和△ABE中
|
∴△ADC≌△ABE(SAS),
∴CD=BE.
∵AB=100m,在直角△ABD中,由勾股定理,得
BD=100
| 2 |
∴CD=
1002+(100
|
| 3 |
∴BE=CD=100
| 3 |
答:BE的长为100
| 3 |
看了 (1)如图1,已知△ABC,...的网友还看了以下:
G都是有机化合物,它们的转化关系如图.已知:6.0g化合物E完全燃烧生成8.8gCO2和3.G都是 2020-04-27 …
芳香族化合物A只有两个对位取代基,在一定条件下有如下图所示转化关系。其中,1molC与Na完全反应 2020-05-02 …
某刑事案件的六个嫌疑分子A,B,C,D,E,F交待了以下材料:AB与F作案;BD与A作案;CB与E 2020-05-16 …
A,B,C,D,E五人小组分工合作解决一项要求20分钟完成的任务,但至完所时多用了2分钟,事后总结 2020-05-17 …
资产净利润率越高,说明企业全部资产的盈利能力越强。该指标与净利润成正比,与资产平均总额( )。A. 2020-05-27 …
晶体管工作在放大区时的偏置状态为().A.b与e极,b与c极间均正向偏置B.b与e极,b与c极间均 2020-07-20 …
A-G都是有机物,它们的转化关系如下:请回答下列问题:(1)已知:6.0g化合物E完全燃烧生成8. 2020-07-29 …
A、B、C、D、E为1~20号元素中的五种,它们的原子中质子数和中子数不等.又已知:①A与D、B与 2020-08-01 …
A、B、C、D、E五人小组分工合作解决一项要求20分钟完成的任务,但至完成任务时多用了2分钟.之后总 2020-12-01 …
信号与系统全响应的问题?初始状态相同,当激励为f1(t)=δ(t)时,全响应y1(t)=δ(t)+e 2020-12-27 …