早教吧作业答案频道 -->数学-->
如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF=.(用含x的代数式表示)②求∠AOC
题目详情
如图,直线AB、CD相交于点O,OE平分∠BOD.
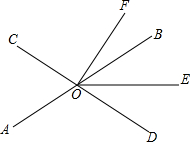
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①则∠EOF=___.(用含x的代数式表示)
②求∠AOC的度数.

(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①则∠EOF=___.(用含x的代数式表示)
②求∠AOC的度数.
▼优质解答
答案和解析
(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF-∠BOD,
∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,
∴∠BOE=
∠BOD=
×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°,
(2)①∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=x,
∵OF平分∠COE,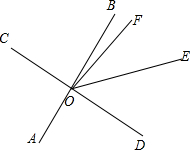
∴∠FOE=
x,
故答案为:
x;
②∵∠BOE=∠FOE-∠FOB,
∴∠BOE=
x-15°,
∵∠BOE+∠AOE=180°,
∴
x-15°+x=180°,
解得:x=130°,
∴∠AOC=2∠BOE=2×(180°-130°)=100°.
∵∠FOB=∠DOF-∠BOD,
∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=∠FOB+∠BOE=35°+20°=55°,
(2)①∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=x,
∵OF平分∠COE,

∴∠FOE=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
②∵∠BOE=∠FOE-∠FOB,
∴∠BOE=
| 1 |
| 2 |
∵∠BOE+∠AOE=180°,
∴
| 1 |
| 2 |
解得:x=130°,
∴∠AOC=2∠BOE=2×(180°-130°)=100°.
看了 如图,直线AB、CD相交于点...的网友还看了以下:
已知abc为三角形三边,且方程a(x²+1)-2bc+c(x+1)(x-1)=0有两个相等实数根, 2020-04-05 …
我在看有理函数的不定积分的时候有些不明白x-3/[(x-1)^2(x-1)]等于了[Ax+B/(x 2020-05-13 …
已知实数a为常数,U=R,设集合A={x|x-3x+1>0},B={x|y=log2x-1},C= 2020-05-13 …
R上的函数f(x),g(x).函数y=f(g(x))有不动点.则函数y=g(f(x))不可能是A. 2020-05-17 …
求问高一二次函数一题设-2x^3-4x^2-x+3=a(x+1)^3+b(x+1)^2+c(x+1 2020-05-20 …
;②2\(x+1)=4\(x+1)-1的解x=1;③3\(x+1)=6\(x+1)-1的解x=2; 2020-05-23 …
下面所给出的算法的时间复杂度为(56)。(n为大于1的数) x=n;y=1; while(x>y*y 2020-05-26 …
lingo怎样求解代数方程如a*w/(1+x)-p-1/(B-c-x)^2=0式中除x是未知数外, 2020-06-06 …
初二的代数难题已知:p+q+r=9,且p/x方-yz=q/y方-zx=r/z方-xy求PX+QY+ 2020-06-12 …
曲线xy=1的参数方程是?A.x=t^(1/2)y=t^(1/2)B.x=sinαy=1/sinα 2020-06-12 …