早教吧作业答案频道 -->数学-->
已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).(1)求抛物线的表达式及顶点坐标;(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;(3)在(2)的条件下,当-2<x<2时,直线
题目详情
已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围.
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围.
▼优质解答
答案和解析
 (1)根据题意得
(1)根据题意得
,
解得
,
所以抛物线的解析式为y=x2-2x-3.
∵抛物线的解析式为y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点坐标为(1,-4).
(2)根据题意,-y=x2-2x-3,所以y=-x2+2x+3.
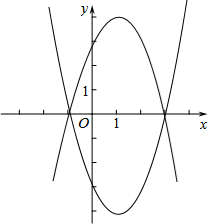
(3)∵抛物线y=x2-2x-3的顶点为(1,-4),当x=-2时,y=5,抛物线y=-x2+2x+3的顶点(1,4),当x=-2时,y=-5.
∴当-2<x<2时,直线y=m与该图象有一个公共点,则m=4或-5<m<3.
 (1)根据题意得
(1)根据题意得
|
解得
|
所以抛物线的解析式为y=x2-2x-3.
∵抛物线的解析式为y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点坐标为(1,-4).
(2)根据题意,-y=x2-2x-3,所以y=-x2+2x+3.
(3)∵抛物线y=x2-2x-3的顶点为(1,-4),当x=-2时,y=5,抛物线y=-x2+2x+3的顶点(1,4),当x=-2时,y=-5.
∴当-2<x<2时,直线y=m与该图象有一个公共点,则m=4或-5<m<3.
看了 已知:抛物线y=x2+bx+...的网友还看了以下:
b取何值时直线x-y+b=0被曲线x^2+y^2=5所截得的弦长为2√3.答案是正负二可是我怎么做 2020-05-13 …
二次函数y=n(n+1)X^2-(2n+1)X+1 ,n=1,2,3.时,其图像在X轴上截得线段长 2020-05-16 …
已知直线l过定点(1,1),则当直线l截圆C:(x+1)^2+(y-2)^2=6所得的弦长最小时已 2020-06-03 …
当α从0到π变化时,曲线x的平方+y的平方cosα=1怎样变化?如上 2020-06-04 …
将曲线log2x+log2y=2沿x、y轴-分别向右平移两个单位,向上平移一个单位,此时直线x+y 2020-06-06 …
将曲线log2x+log2y=2沿x、y轴-分别向右平移两个单位,向上平移一个单位,此时直线x+y 2020-06-06 …
不论m取何数时,直线x+3m=y与y=-x+1的交点不可能在哪个象限?呜呜.一次函数跟2元一次方程 2020-07-15 …
当m为何值时,直线x-y+m=0与圆x^2+y^2=4相交,相切,相离 2020-07-31 …
当a为何值时,直线x+y-2a+1=0与圆x^2+y^2-2x+4y+1=0相切?相离?相交? 2020-07-31 …
当M为参数时,集合A={(x,y)|x^2+y^2+x-6*y+m=0}是以(-1/2,3)为圆心的 2020-12-27 …