早教吧作业答案频道 -->数学-->
如图,在Rt△ABC和Rt△ABD中,∠C=∠BAD=90°,BD、AC交于点F,且AF=AD,作DE⊥AC于点E.(1)求证:∠CBF=∠ABF;(2)若AB-BC=4,AC=8,求BC的长;(3)求证:AE=CF.
题目详情
如图,在Rt△ABC和Rt△ABD中,∠C=∠BAD=90°,BD、AC交于点F,且AF=AD,作DE⊥AC于点E.
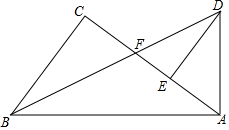
(1)求证:∠CBF=∠ABF;
(2)若AB-BC=4,AC=8,求BC的长;
(3)求证:AE=CF.

(1)求证:∠CBF=∠ABF;
(2)若AB-BC=4,AC=8,求BC的长;
(3)求证:AE=CF.
▼优质解答
答案和解析
(1)证明:∵AF=AD,
∴∠ADF=∠AFD,
∵∠AFD=∠BFC,
∴∠ADF=∠BFC,
在Rt△CBF和Rt△ABD中,
∴Rt△CBF~Rt△ABD,
∴∠CBF=∠ABF.
(2) 设BC=x,
∵AB-BC=4,
∴AB=x+4,
在Rt△ABC中,
∵AC=8,
∴(x+4)2-x2=64,
整理,可得
8x+16=64,
解得x=6,
∴BC的长是6.
(3)证明:如图1,作FG⊥AB于点G,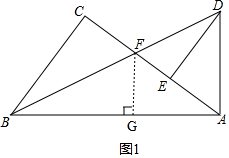 ,
,
∵∠CBF=∠ABF,
∴FG=CF,
∵∠FAG+∠DAE=90°,∠ADE+∠DAE=90°,
∴∠FAG=∠ADE,
∵∠AFG=90°-∠FAG,∠DAE=90°-∠ADE,
∴∠AFG=∠DAE,
在Rt△AFG和Rt△DAE中,
∴Rt△AFG≌Rt△DAE,
∴AE=FG,
∵FG=CF,
∴AE=CF.
∴∠ADF=∠AFD,
∵∠AFD=∠BFC,
∴∠ADF=∠BFC,
在Rt△CBF和Rt△ABD中,
|
∴Rt△CBF~Rt△ABD,
∴∠CBF=∠ABF.
(2) 设BC=x,
∵AB-BC=4,
∴AB=x+4,
在Rt△ABC中,
∵AC=8,
∴(x+4)2-x2=64,
整理,可得
8x+16=64,
解得x=6,
∴BC的长是6.
(3)证明:如图1,作FG⊥AB于点G,
 ,
,∵∠CBF=∠ABF,
∴FG=CF,
∵∠FAG+∠DAE=90°,∠ADE+∠DAE=90°,
∴∠FAG=∠ADE,
∵∠AFG=90°-∠FAG,∠DAE=90°-∠ADE,
∴∠AFG=∠DAE,
在Rt△AFG和Rt△DAE中,
|
∴Rt△AFG≌Rt△DAE,
∴AE=FG,
∵FG=CF,
∴AE=CF.
看了 如图,在Rt△ABC和Rt△...的网友还看了以下:
∮1dx/(x^2+y^2+z^2)ds,其中,曲线x=(e^t)sinty==(e^t)cost 2020-06-03 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
已知函数f(x)=1/2ax2+2x,g(x)=Inx.是否存在正实数a,使得函数T(x)=g(x 2020-07-22 …
高数题,定积分高数题设A=∫[1,0]=(e^t)/(1+t),用A表示I=∫[a,a-1](e^ 2020-07-30 …
设函数f(x)=alnx-bx^2(x>0)(1)若函数f(x)在x=1处与直线y=-1/2相切, 2020-07-31 …
关于参数方程的问题1.x=e^t+e^(-t)y=2(e^t-e^(-t))e=2.71828(t 2020-08-02 …
编译原理题目5、设有文法(E):E→E+T|TT→T*F|FF→(E)|i1)该文法含有左递归吗?若 2020-11-23 …
你好请教两个考研数学问题~设b大于a大于e证明存在一个t属于(a,b),使得be^a-ae^b=(1 2020-11-26 …
2-1设文法G[E]的产生式集为:EàE+T|E-T|TTàT*F|T/F|FFà(E)|i(1)给 2020-11-26 …
已知文法G:(1)E→E+T|T(2)T→T*F|F(3)F→P↑F|P(4)P→(E)|i1.已知 2020-12-07 …