如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②AMAB=ANAC；③△PMN为等边三角形；④当∠ABC=45°时，BN=2PC．其中正确的个数是（）A.1

Question

如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②

(AM)/(AB)=(AN)/(AC)；③△PMN为等边三角形；④当∠ABC=45°时，BN=√(2)PC．其中正确的个数是（　　）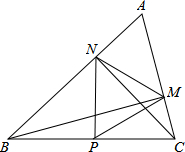

A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

①∵BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，
∴PM=(1)/(2)BC，PN=(1)/(2)BC，
∴PM=PN，正确；

②在△ABM与△ACN中，
∵∠A=∠A，∠AMB=∠ANC=90°，
∴△ABM∽△ACN，
∴(AM)/(AB)=(AN)/(AC)，正确；

③∵∠A=60°，BM⊥AC于点M，CN⊥AB于点N，
∴∠ABM=∠ACN=30°，
在△ABC中，∠BCN+∠CBM═180°-60°-30°×2=60°，
∵点P是BC的中点，BM⊥AC，CN⊥AB，
∴PM=PN=PB=PC，
∴∠BPN=2∠BCN，∠CPM=2∠CBM，
∴∠BPN+∠CPM=2（∠BCN+∠CBM）=2×60°=120°，
∴∠MPN=60°，
∴△PMN是等边三角形，正确；

④当∠ABC=45°时，∵CN⊥AB于点N，
∴∠BNC=90°，∠BCN=45°，
∴BN=CN，
∵P为BC边的中点，
∴PN⊥BC，△BPN为等腰直角三角形
∴BN=√(2)PB=√(2)PC，正确．
故选D．