如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°<θ<90°），PM、PN分别

Question

如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°<θ<90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是___．

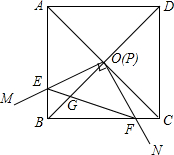
（1）EF= √(2)OE；（2）S_{四边形OEBF}：S_{正方形ABCD}=1：4；（3）BE+BF= √(2)OA；（4）在旋转过程中，当△BEF与△COF的面积之和最大时，AE= (3)/(4)；（5）OG•BD=AE²+CF²．

Answer 1

（1）∵四边形ABCD是正方形，
∴OB=OC，∠OBE=∠OCF=45°，∠BOC=90°，
∴∠BOF+∠COF=90°，
∵∠EOF=90°，
∴∠BOF+∠COE=90°，
∴∠BOE=∠COF，
在△BOE和△COF中，

∠BOE=∠COF

OB=OC

∠OBE=∠OCF

，
∴△BOE≌△COF（ASA），
∴OE=OF，BE=CF，
∴EF=√(2)OE；故正确；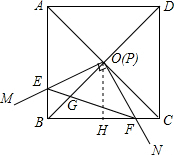

（2）∵S_{四边形OEBF}=S_△BOE+S_△BOE=S_△BOE+S_△COF=S_△BOC=(1)/(4)S_{正方形ABCD}，
∴S_{四边形OEBF}：S_{正方形ABCD}=1：4；故正确；

（3）∴BE+BF=BF+CF=BC=√(2)OA；故正确；

（4）过点O作OH⊥BC，
∵BC=1，
∴OH=(1)/(2)BC=(1)/(2)，
设AE=x，则BE=CF=1-x，BF=x，
∴S_△BEF+S_△COF=(1)/(2)BE•BF+(1)/(2)CF•OH=(1)/(2)x（1-x）+(1)/(2)（1-x）×(1)/(2)=-(1)/(2)（x-(1)/(4)）²+(9)/(32)，
∵a=-(1)/(2)<0，
∴当x=(1)/(4)时，S_△BEF+S_△COF最大；
即在旋转过程中，当△BEF与△COF的面积之和最大时，AE=(1)/(4)；故错误；

（5）∵∠EOG=∠BOE，∠OEG=∠OBE=45°，
∴△OEG∽△OBE，
∴OE：OB=OG：OE，
∴OG•OB=OE²，
∵OB=(1)/(2)BD，OE=

√(作业帮用户2017-02-06扫描下载二维码©2019 作业帮 联系方式：[e-mail]作业帮协议)