早教吧作业答案频道 -->数学-->
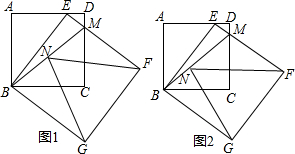
如图1,正方形ABCD中,点E为AD上任意一点,连接BE,以BE为边向BE右侧作正方形BEFG,EF交CD于点M,连接BM,N为BM的中点,连接GN,FN.(1)若AB=4,AE:DE=3:1,求EM的长;(2)求证:GN=FN;(3)
题目详情
如图1,正方形ABCD中,点E为AD上任意一点,连接BE,以BE为边向BE右侧作正方形BEFG,EF交CD于点M,连接BM,N为BM的中点,连接GN,FN.
(1)若AB=4,AE:DE=3:1,求EM的长;
(2)求证:GN=FN;
(3)如图2,移动点E,使得FN⊥CD于点Q时,请探究CM与DE的数量关系并说明理由.
(1)若AB=4,AE:DE=3:1,求EM的长;
(2)求证:GN=FN;
(3)如图2,移动点E,使得FN⊥CD于点Q时,请探究CM与DE的数量关系并说明理由.

▼优质解答
答案和解析
(1)∵AB=4,AE:DE=3:1,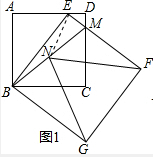
∴AE=3,DE=1,
∴BE=
=5,
∵∠BEF=90°,∠BEF=90°,∠BEF=90°,
∴△ABE∽△DEM,
∴
=
,即
=
,
解得,EM=
;
(2)连接EN,
∵∠BEF=90°,N为BM的中点,
∴EN=
BM=BN=NM,
∴∠NBE=∠NEB,
∴∠NBG=∠NEF,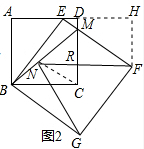
在△NBG和△NEF中,
,
∴△NBG≌△NEF,
∴GN=FN;
(3)如图2,延长ED,过点F作FH⊥ED,交ED的延长线于H,
∵∠BCD=90°,N为BM的中点,
∴CN=
BM=BN=NM,
∵FN⊥CD,
∴CR=MR=
CM,
∵∠A=∠H=90°,
∴∠ABE+∠AEB=90°,
∵∠BEF=90°,
∴∠AEB+∠FEH=90°,
∴∠ABE=∠FEH,
在△ABE和△HEF中,
,
∴△ABE≌△HEF,
∴AE=HF,
∵∠H=∠RDH=∠DRF=90°,
∴四边形DRFH是矩形,
∴AE=HF=DR,
∴AD-AE=CD=DR,即DE=CR,
∴DE=
CM.

∴AE=3,DE=1,
∴BE=
| AB2+AE2 |
∵∠BEF=90°,∠BEF=90°,∠BEF=90°,
∴△ABE∽△DEM,
∴
| AB |
| DE |
| BE |
| EM |
| 4 |
| 1 |
| 5 |
| EM |
解得,EM=
| 5 |
| 4 |
(2)连接EN,
∵∠BEF=90°,N为BM的中点,
∴EN=
| 1 |
| 2 |
∴∠NBE=∠NEB,
∴∠NBG=∠NEF,

在△NBG和△NEF中,
|
∴△NBG≌△NEF,
∴GN=FN;
(3)如图2,延长ED,过点F作FH⊥ED,交ED的延长线于H,
∵∠BCD=90°,N为BM的中点,
∴CN=
| 1 |
| 2 |
∵FN⊥CD,
∴CR=MR=
| 1 |
| 2 |
∵∠A=∠H=90°,
∴∠ABE+∠AEB=90°,
∵∠BEF=90°,
∴∠AEB+∠FEH=90°,
∴∠ABE=∠FEH,
在△ABE和△HEF中,
|
∴△ABE≌△HEF,
∴AE=HF,
∵∠H=∠RDH=∠DRF=90°,
∴四边形DRFH是矩形,
∴AE=HF=DR,
∴AD-AE=CD=DR,即DE=CR,
∴DE=
| 1 |
| 2 |
看了 如图1,正方形ABCD中,点...的网友还看了以下:
在四边形ABCD中,AD=BC,M,N各是AB,DC的中点,延长AD与MN延长线交于点E,延长BC 2020-05-16 …
1.已知:如图,O正方形ABCD的中心…………1.已知:如图,O正方形ABCD的中心,BE平分∠D 2020-05-16 …
如图,△ABC的顶点A.B在圆O上,且AC过弧AB的中点D,过点D作圆O的切线DE交BC于点E,延 2020-06-05 …
如图,矩形ABCD中,点O是AC的中点,AC=2AB.延长AB至G.使BG=AB.连接G.O交于点 2020-07-22 …
(2012•莆田)(1)如图①,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D.求证:AB2 2020-07-27 …
在矩形ABCD中,AD=10,AB=8,点E在长AD上,点F在BC上,若矩形EFCD相似BCDA, 2020-07-30 …
初二相似图形,如图,在四边形ABCD中,延长AB到点E,延长AD到点G,链接AC并延长到点F,使得 2020-08-01 …
如图,已知点E是长方形ABCD中AD边上一点,将四边形BCDE沿直线BE折叠,折叠后点C的对应点为 2020-08-02 …
在圆内接四边形ABCD中,延长AB,DC交与点E,延长AD,BC交与点F,若∠E=20,∠F=40 2020-08-03 …
(2012•莆田)(1)如图①,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D.求证:AB2= 2020-11-12 …