早教吧作业答案频道 -->数学-->
如图,一次函数y=-x+b与反比例函数y=4x(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.(1)用含m的代数式表示出b
题目详情
如图,一次函数y=-x+b与反比例函数y=
(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
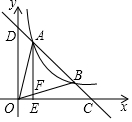
(1)用含m的代数式表示出b;
(2)若S△OAF+S四边形EFBC=4,求m的值.
| 4 |
| x |

(1)用含m的代数式表示出b;
(2)若S△OAF+S四边形EFBC=4,求m的值.
▼优质解答
答案和解析
(1)∵点A在反比例函数y=
(x>0)的图象上,且点A的横坐标为m,
∴点A的纵坐标为
,即点A的坐标为(m,
).
令一次函数y=-x+b中x=m,则y=-m+b,
∴-m+b=
即b=m+
.
(2)作AM⊥OD于M,BN⊥OC于N.
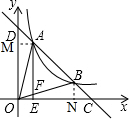
∵反比例函数y=
、一次函数y=-x+b都是关于直线y=x对称,
∴AD=BC,OD=OC,DM=AM=BN=CN,记△AOF面积为S,
则△OEF面积为2-S,四边形EFBC面积为4-S,△OBC和△OAD面积都是6-2S,△ADM面积为4-2S=2(2-s),
∴S△ADM=2S△OEF,
由对称性可知AD=BC,OD=OC,∠ODC=∠OCD=45°,△AOM≌△BON,AM=NB=DM=NC,
∴EF=
AM=
NB,
∴EF是△OBN的中位线,
∴N(2m,0),
∴点B坐标(2m,
)代入直线y=-x+m+
,
∴
=-2m+m+
,整理得到m2=2,
∵m>0,
∴m=
.
| 4 |
| x |
∴点A的纵坐标为
| 4 |
| m |
| 4 |
| m |
令一次函数y=-x+b中x=m,则y=-m+b,
∴-m+b=
| 4 |
| m |
即b=m+
| 4 |
| m |
(2)作AM⊥OD于M,BN⊥OC于N.

∵反比例函数y=
| 4 |
| x |
∴AD=BC,OD=OC,DM=AM=BN=CN,记△AOF面积为S,
则△OEF面积为2-S,四边形EFBC面积为4-S,△OBC和△OAD面积都是6-2S,△ADM面积为4-2S=2(2-s),
∴S△ADM=2S△OEF,
由对称性可知AD=BC,OD=OC,∠ODC=∠OCD=45°,△AOM≌△BON,AM=NB=DM=NC,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF是△OBN的中位线,
∴N(2m,0),
∴点B坐标(2m,
| 2 |
| m |
| 4 |
| m |
∴
| 2 |
| m |
| 4 |
| m |
∵m>0,
∴m=
| 2 |
看了 如图,一次函数y=-x+b与...的网友还看了以下:
直线y=kx+号2与根反比例函数y=2根号2/x(x>0)的图象交于点A,与坐标轴分别交于点M、N 2020-06-07 …
在平面直角坐标系中,抛物线y=-x^2+bx+c的对称轴为直线x=3/2,与坐标轴交于A、B、C三 2020-06-10 …
椭圆C:x^2/m+y^2/(8-m)=1(1)若椭圆C的焦点在x轴上,求m的取值范围(2)若m= 2020-06-12 …
如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,现有以下结论:①当x=-2时 2020-06-14 …
①1)直线y=kx-4与与坐标轴相交围成的三角形面积是6,求k值2)直线y=-2x+b与与坐标轴相 2020-06-14 …
已知:一次函数y=3/2x+m 如果它的图像经过第一三四象限,且与坐标轴围成的三角形面积为27,求 2020-06-27 …
如图,直线l:y=-12x+1与坐标轴交于A,B两点,点M(m,0)是x轴上一动点,以点M为圆心, 2020-07-14 …
关于x的函数y=2mx2+(1-m)x-1-m(m是实数),探索发现了以下四条结论:①函数图象与坐 2020-07-17 …
如图,在平面直角坐标系中,抛物线C1:y=m(x-2)2与坐标轴交于A、B两点,点P(-3,0), 2020-07-26 …
如图,直线y=-43x+4与坐标轴分别交于点M、N.(1)求M,N两点的坐标;(2)若点P在坐标轴上 2020-11-01 …