早教吧作业答案频道 -->数学-->
已知直线l:(m+2)x+(m-1)y+4-4m=0上总存在点M,使得过M点作的圆C:x2+y2+2x-4y+3=0的两条切线互相垂直,则实数m的取值范围是()A.m≤1或m≥2B.2≤m≤8C.-2≤m≤10D.m≤-2或m≥8
题目详情
已知直线l:(m+2)x+(m-1)y+4-4m=0上总存在点M,使得过M点作的圆C:x2+y2+2x-4y+3=0的两条切线互相垂直,则实数m的取值范围是( )
A. m≤1或m≥2
B. 2≤m≤8
C. -2≤m≤10
D. m≤-2或m≥8
▼优质解答
答案和解析
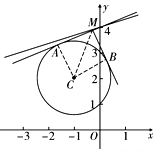 如图,设切点分别为A,B.连接AC,BC,MC,
如图,设切点分别为A,B.连接AC,BC,MC,
由∠AMB=∠MAC=∠MBC=90°及MA=MB知,四边形MACB为正方形,故|MC|=
=2,
若直线l上总存在点M使得过点M的两条切线互相垂直,只需圆心(-1,2)到直线l的距离d=
≤2,即m2-8m-20≤0,∴-2≤m≤10,
故选:C.
 如图,设切点分别为A,B.连接AC,BC,MC,
如图,设切点分别为A,B.连接AC,BC,MC,由∠AMB=∠MAC=∠MBC=90°及MA=MB知,四边形MACB为正方形,故|MC|=
| 2+2 |
若直线l上总存在点M使得过点M的两条切线互相垂直,只需圆心(-1,2)到直线l的距离d=
| |-m-2+2m-2+4-4m| | ||
|
故选:C.
看了 已知直线l:(m+2)x+(...的网友还看了以下:
案例分析题六(本题10分)甲公司是一家能源化工股份有限公司,已在上海证券交易所上市.该公司2007年 2020-05-19 …
∫1在上0在下(2x^2+1)^3dx=229/35 2020-06-14 …
.已知f(x)=xlgx,那么f(x)A、在(0,e)上单调递增B、在(0,10)上单调递增C、在 2020-07-12 …
````重赏!1.已知A(8,0),B(0,6)线段AB上的点P在X轴上的射影为Q(a,o),若三 2020-07-30 …
已知定义在(-∞,0)U(0,+∞)上的奇函数f(x)满足f(2)=0,且在(-∞,0)上是增函数 2020-08-01 …
1.已知分段函数f(x)是奇函数,当X∈[0,+∞)时的解析式为y=x^2(X的平方),求这个函数 2020-08-01 …
“量贩”源于1963年法国的一家超大型类似超级市场的大卖场,后来日本把这种购物经营业态叫做量贩,日 2020-08-04 …
4月27日晚,四川广元18岁的蒲某拨通上海国航电话,称已在上海飞往成都的国航CA406航班上安放了炸 2020-11-12 …
英语翻译在南京教书之前这个教授已在上海工作多年.需要两种不同的译法 2020-11-23 …
人工降雨①人工消雨,其实就是人工降雨。这次东亚运动会的消雨指挥部已在上海以西的太湖地区30~100千 2020-11-23 …