早教吧作业答案频道 -->数学-->
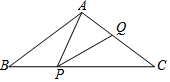
如图,在△ABC中,己知AB=AC=5cm,BC=8cm,点P在边BC上沿B到C的方向以每秒1cm的速度运动(不与点B,C重合),点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t=.
题目详情
如图,在△ABC中,己知AB=AC=5 cm,BC=8 cm,点P在边BC上沿B到C的方向以每秒1 cm的速度运动(不与点B,C重合),点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t=___.

▼优质解答
答案和解析
①如图1中,当PA=PQ时,作AF⊥BC于F,PE⊥AC于E.
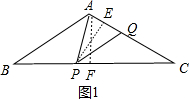
∵AB=AC=5,AF⊥BC,BC=8,
∴BF=CF=4,∠B=∠C,
∵∠APC=∠B+∠BAP=∠APQ+∠QPC,
∵∠APQ=∠B,
∴∠BAP=∠QPC,
∴△BAP∽△CPQ,
∴
=
,
∴
=
,
∴CQ=
,
∵PA=PQ,PE⊥AQ,
∴AE=EQ=
[5-
],
∵cos∠C=
=
,
∴
=
,
解得t=3或13(舍弃)
②如图2中,当QA=QP时,作PE⊥AC于E.
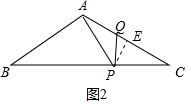
∵QA=QP,
∴∠QAP=∠QPA=∠C,
∴PA=PC,∵PE⊥AC,
∴AE=EC=
,
由cos∠C=
=
,得到
=
,解得t=
,
综上所述,t=3秒或
秒时,△PQA是等腰三角形.
故答案为3秒或
秒.

∵AB=AC=5,AF⊥BC,BC=8,
∴BF=CF=4,∠B=∠C,
∵∠APC=∠B+∠BAP=∠APQ+∠QPC,
∵∠APQ=∠B,
∴∠BAP=∠QPC,
∴△BAP∽△CPQ,
∴
| AB |
| PC |
| BP |
| CQ |
∴
| 5 |
| 8-t |
| t |
| CQ |
∴CQ=
| t(8-t) |
| 5 |
∵PA=PQ,PE⊥AQ,
∴AE=EQ=
| 1 |
| 2 |
| t(8-t) |
| 5 |
∵cos∠C=
| EC |
| PC |
| 4 |
| 5 |
∴
| ||||||
| 8-t |
| 4 |
| 5 |
解得t=3或13(舍弃)
②如图2中,当QA=QP时,作PE⊥AC于E.

∵QA=QP,
∴∠QAP=∠QPA=∠C,
∴PA=PC,∵PE⊥AC,
∴AE=EC=
| 5 |
| 2 |
由cos∠C=
| EC |
| PC |
| 4 |
| 5 |
| ||
| 8-t |
| 4 |
| 5 |
| 39 |
| 8 |
综上所述,t=3秒或
| 39 |
| 8 |
故答案为3秒或
| 39 |
| 8 |
看了 如图,在△ABC中,己知AB...的网友还看了以下:
人口增长率问题(微分方程问题)已知人口增长速度与人口的数量成正比.设人口增长率关于时间t的函数为f 2020-04-25 …
已知椭圆T的方程为x^2/a^2+y^2/b^2=1(a>b>0),A(0,b),B(0,-b)和 2020-04-27 …
在坐标平面上有两个区域M和N,M是由y≥0、y≤x和y≤2-x三个不等式来确定的,N是随t变化的区 2020-05-13 …
设r、s、t是三次方程8X³+1001X+2008=0的三个根,则(r+s)³+(s+t)³+(t 2020-05-14 …
已知,如图一,在RT△ACB中,∠C=90°,AC=4CM,BC=3CM,点P由B出发沿BA方向向 2020-06-05 …
设x=[√(t+1)-√t]/[√(t+1)+√t],y=[√(t+1)+√t]/[√(t+1)- 2020-06-11 …
设函数f(x)=-cos²x-4tsinx/2cosx/2+2t²-6t+2,x∈R.其中|t|≤ 2020-06-27 …
△ABC是一个直角三角形,其中∠C=90゜,∠A=30゜,BC=6;O为AB上一点,且OB=3,⊙ 2020-07-31 …
已知椭圆C的中心在坐标原点,离心率e=根号三/2,一个焦点的坐标为(根号三,0)①求椭圆C的方程② 2020-08-01 …
已知函数f(x)=x^3-x(1)求曲线y=f(x)在M(t,f(t))处(2)设a>0,如果过点P 2020-11-03 …