早教吧作业答案频道 -->数学-->
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中点A的坐标为(-3,0),点C为抛物线与y轴的交点.(1)求点B的坐标;(2)求此抛物线的解析式;(3)若点P在抛物线上,
题目详情
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中点A的坐标为(-3,0),点C为抛物线与y轴的交点.
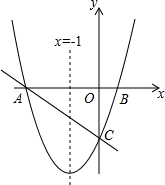
(1)求点B的坐标;
(2)求此抛物线的解析式;
(3)若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;
(4)设点Q为线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.

(1)求点B的坐标;
(2)求此抛物线的解析式;
(3)若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;
(4)设点Q为线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
▼优质解答
答案和解析
(1)∵对称轴为直线x=-1的抛物线y=x2+bx+c(a≠0)与x轴相交于A、B两点,
∴A、B两点关于直线x=-1对称,
∵点A的坐标为(-3,0),
∴点B的坐标为(1,0);
(2)∵抛物线y=x2+bx+c的对称轴为直线x=-1,
∴-
=-1,解得b=2.
将B(1,0)代入y=x2+2x+c,
得1+2+c=0,解得c=-3.
则二次函数的解析式为y=x2+2x-3;
(3)由(2)可知C(0,-3),
∴OC=3,
设P点坐标为(x,x2+2x-3),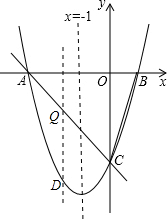
∵S△POC=4S△BOC,
∴
×3×|x|=4×
×3×1,
∴|x|=4,x=±4.
当x=4时,x2+2x-3=16+8-3=21;
当x=-4时,x2+2x-3=16-8-3=5.
∴点P的坐标为(4,21)或(-4,5);
(4)设直线AC的解析式为y=kx+t (k≠0)将A(-3,0),C(0,-3)代入,
得
,解得
,
∴直线AC的解析式为y=-x-3.
设Q点坐标为(x,-x-3)(-3≤x≤0),则D点坐标为(x,x2+2x-3),
QD=(-x-3)-(x2+2x-3)=-x2-3x=-(x+
)2+
,
∴当x=-
时,QD有最大值
.
(1)∵对称轴为直线x=-1的抛物线y=x2+bx+c(a≠0)与x轴相交于A、B两点,
∴A、B两点关于直线x=-1对称,
∵点A的坐标为(-3,0),
∴点B的坐标为(1,0);
(2)∵抛物线y=x2+bx+c的对称轴为直线x=-1,
∴-
| b |
| 2 |
将B(1,0)代入y=x2+2x+c,
得1+2+c=0,解得c=-3.
则二次函数的解析式为y=x2+2x-3;
(3)由(2)可知C(0,-3),
∴OC=3,
设P点坐标为(x,x2+2x-3),

∵S△POC=4S△BOC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴|x|=4,x=±4.
当x=4时,x2+2x-3=16+8-3=21;
当x=-4时,x2+2x-3=16-8-3=5.
∴点P的坐标为(4,21)或(-4,5);
(4)设直线AC的解析式为y=kx+t (k≠0)将A(-3,0),C(0,-3)代入,
得
|
|
∴直线AC的解析式为y=-x-3.
设Q点坐标为(x,-x-3)(-3≤x≤0),则D点坐标为(x,x2+2x-3),
QD=(-x-3)-(x2+2x-3)=-x2-3x=-(x+
| 3 |
| 2 |
| 9 |
| 4 |
∴当x=-
| 3 |
| 2 |
| 9 |
| 4 |
看了 如图,对称轴为直线x=-1的...的网友还看了以下:
已知两条直线l1:7x+8y+9=0和l2:7x+8Y-3=0已知直线L1和L2的方程分别是7X+ 2020-05-16 …
已知直线L1和L2的方程分别为7x+8y+9=0,7x+8y-3=0,直线L与L1的距离为d1,与 2020-05-16 …
直线与圆的方程,位置关系1.经点A(2,1)且在Y轴上截距为3的直线方程是____________ 2020-05-17 …
直径60的孔上偏差为0.046.下偏差为0.直径六十轴的上偏差为-0.030下偏差为-0.060! 2020-06-25 …
直径60的孔上偏差为0.046.下偏差为0.直径六十轴的上偏差为-0.030下偏差为-0.060! 2020-06-25 …
当B=0A不等于0时,直线Ax+By+c=0化成Ax+c=0此时直线与?轴垂直,轴平行或?直线的倾 2020-07-30 …
已知圆O:x2+y2=4,点P是直线X=4上的动点,若点A(-2,0),B(2,0),直线PA,P 2020-07-30 …
已知:圆C:x^2+y^2-8y+12=0,直l:ax+y+2a=0.(1)当a为何值时,直线l与 2020-07-31 …
设椭圆(a>b>0)的左焦点为F,上顶点为A,直线AF的倾斜角为45°,(1)求椭圆的离心率;(2 2020-07-31 …
《公司理财》计算题非常着急1、已知某企业某生产线投资3000万元,当年投产,设年销售收入1000万元 2020-11-06 …