早教吧作业答案频道 -->数学-->
如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,(Ⅰ)若D为线段AC的中点,求证;AC⊥平面PDO;(Ⅱ)求三棱锥P-ABC体积的最大值;(Ⅲ)若BC=2,点E在线
题目详情
如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,
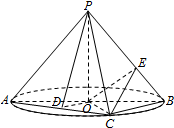
(Ⅰ)若D为线段AC的中点,求证;AC⊥平面PDO;
(Ⅱ)求三棱锥P-ABC体积的最大值;
(Ⅲ)若BC=
,点E在线段PB上,求CE+OE的最小值.

(Ⅰ)若D为线段AC的中点,求证;AC⊥平面PDO;
(Ⅱ)求三棱锥P-ABC体积的最大值;
(Ⅲ)若BC=
| 2 |
▼优质解答
答案和解析
(Ⅰ)在△AOC中,因为OA=OC,D为AC的中点,
所以AC⊥DO,
又PO垂直于圆O所在的平面,
所以PO⊥AC,
因为DO∩PO=O,
所以AC⊥平面PDO.
(Ⅱ)因为点C在圆O上,
所以当CO⊥AB时,C到AB的距离最大,且最大值为1,
又AB=2,所以△ABC面积的最大值为
×2×1=1,
又因为三棱锥P-ABC的高PO=1,
故三棱锥P-ABC体积的最大值为:
×1×1=
.
(Ⅲ)在△POB中,PO=OB=1,∠POB=90°,
所以PB=
=
,
同理PC=
,所以PB=PC=BC,
在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图所示,
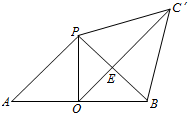 当O,E,C′共线时,CE+OE取得最小值,
当O,E,C′共线时,CE+OE取得最小值,
又因为OP=OB,C′P=C′B,
所以OC′垂直平分PB,即E为PB中点.
从而OC′=OE+EC′=
+
=
.
亦即CE+OE的最小值为:
.
所以AC⊥DO,
又PO垂直于圆O所在的平面,
所以PO⊥AC,
因为DO∩PO=O,
所以AC⊥平面PDO.
(Ⅱ)因为点C在圆O上,

所以当CO⊥AB时,C到AB的距离最大,且最大值为1,
又AB=2,所以△ABC面积的最大值为
| 1 |
| 2 |
又因为三棱锥P-ABC的高PO=1,
故三棱锥P-ABC体积的最大值为:
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅲ)在△POB中,PO=OB=1,∠POB=90°,
所以PB=
| 12+12 |
| 2 |
同理PC=
| 2 |
在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图所示,
 当O,E,C′共线时,CE+OE取得最小值,
当O,E,C′共线时,CE+OE取得最小值,又因为OP=OB,C′P=C′B,
所以OC′垂直平分PB,即E为PB中点.
从而OC′=OE+EC′=
| ||
| 2 |
| ||
| 2 |
| ||||
| 2 |
亦即CE+OE的最小值为:
| ||||
| 2 |
看了 如图,AB是圆O的直径,点C...的网友还看了以下:
如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1,点E、F分别 2020-05-13 …
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为C 2020-07-27 …
如图,已知正四棱锥S-ABCD所有棱长都为1,点E是侧棱SC上一动点,过点E垂直于SC的截面将正四 2020-07-29 …
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=根号3,BC=1, 2020-07-31 …
(2014•天津)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD= 2020-07-31 …
立体几何求三棱锥体积极值正方体ABCD-A1B1C1D1边长为1,EF是棱D1C1上任意两点,EF 2020-08-01 …
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF 2020-08-02 …
正二十面体的面是正三角形,每一个顶点为其一端都有五条棱,则其顶点数V和棱数E的值为()A.V==30 2020-11-18 …
十八世纪瑞士数学家欧拉证明了简单多面体中面数(f)、顶点数(v)棱数(e)之间存在的一个有趣的关系式 2020-11-18 …
已知四棱锥P-ABCD中,底面ABCD为正方形,PC⊥平面ABCD,AB=1,PC=2,E为侧棱PC 2020-12-23 …