如图，在钝角△ABC中，点D是BC的中点，分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF，M、N分别为AB、AC的中点，连接DM、DN、DE、DF、EM、EF、FN．求证：（1）△EMD

Question

如图，在钝角△ABC中，点D是BC的中点，分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF，M、N分别为AB、AC的中点，连接DM、DN、DE、DF、EM、EF、FN．求证：

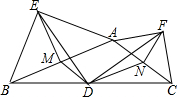
（1）△EMD≌△DNF；
（2）△EMD∽△EAF；
（3）DE⊥DF．

Answer 1

（1）∵D是BC中点，M是AB中点，N是AC中点，
∴DM、DN都是△ABC的中位线，
∴DM∥AC，且DM=(1)/(2)AC；
DN∥AB，且DN=(1)/(2)AB；
∵△ABE是等腰直角三角形，M是AB的中点，
∴EM平分∠AEB，EM=(1)/(2)AB，
∴EM=DN，
同理：DM=FN，
∵DM∥AC，DN∥AB，
∴四边形AMDN是平行四边形，
∴∠AMD=∠AND，
又∵∠EMA=∠FNA=90°，
∴∠EMD=∠DNF，
在△EMD和△DNF中，

EM=DN

∠EMD=∠DNF

MD=NF

，
∴△EMD≌△DNF；
（2）∵三角形ABE是等腰直角三角形，M是AB的中点，
∴EM平分∠AEB，EM⊥AB，
∴EM=MA，∠EMA=90°，∠AEM=∠EAM=45°，
∴(EM)/(EA)=sin45°=(√(2))/(2)，
∵D是BC中点，M是AB中点，
∴DM是△ABC的中位线，
∴DM∥AC，且DM=(1)/(2)AC；
∵△ACF是等腰直角三角形，N是AC的中点，
∴FN=(1)/(2)AC，∠FNA=90°，∠FAN=∠AFN=45°，
又∵DM=(1)/(2)AC，
∴DM=FN=(√(2))/(2)FA，
∵∠EMD=∠EMA+∠AMD=90°+∠AMD，
∠EAF=360°-∠EAM-∠FAN-∠BAC，
=360°-45°-45°-（180°-∠AMD）
=90°+∠AMD，
∴∠EMD=∠EAF，
在△EMD和△∠EAF中，

(EM)/(EA)=(DM)/(FA)=(√(2))/(2)

∠EMD=∠EAF

∴△EMD∽△∠EAF；
（3）∵△EMD∽△∠EAF，
∴∠MED=∠AEF，
∵∠MED+∠AED=45°，
∴∠AED+∠AEF=45°，
即∠DEF=45°，
又∵△EMD≌△DNF，

作业帮用户 2017-02-02