如图，在四棱锥P―ABCD中，底面ABCD是菱形，∠ABC=60°，PA=AC=a，PB=PD=，点E，F分别在PD，BC上，且PE：ED=BF：FC。（1）求证：PA

Question

如图，在四棱锥 P ― ABCD 中，底面 ABCD 是菱形，∠ ABC=60 °， PA=AC=a ， PB=PD= ，点 E ， F 分别在 PD ， BC 上，且 PE ： ED=BF ： FC 。

   （ 1 ）求证： PA ⊥平面 ABCD ；

   （ 2 ）求证： EF// 平面 PAB 。

Answer 1

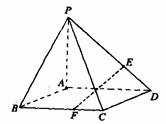
证明：（ 1 ）∵底面 ABCD 是菱形，∠ ABC=60 °，

∴ AB=AD=AC=a. 在△ PAB 中，

∵ PA ² +AB ² =2a ² =PB ²

∴ PA ⊥ AB ，同时 PA ⊥ AD ，又 AB AD=A ，

∴ PA ⊥平面 ABCD

（ 2 ）作 EG//PA 交 AD 于 G ，连接 GF.

则

∴ GF//AB.

又 PA AB=A ， EG GF=G ，

∴平面 EFG// 平面 PAB ，

又 EF 平面 EFG ，

∴ EF// 平面 PAB.