早教吧作业答案频道 -->数学-->
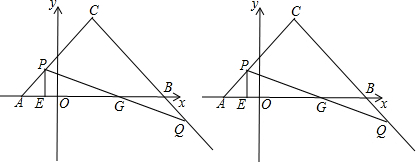
如图,在平面直角坐标系中,已知C(2,4),在x轴的负半轴上取点A(m-3,0),在x轴的正半轴上取点B(4m+2,0),O为原点,AC=BC.(1)求m的值;(2)动点P由点A出发沿AC向点C运动,同时点Q
题目详情
如图,在平面直角坐标系中,已知C(2,4),在x轴的负半轴上取点A(m-3,0),在x轴的正半轴上取点B(4m+2,0),O为原点,AC=BC.
(1)求m的值;
(2)动点P由点A出发沿AC向点C运动,同时点Q由点B出发,以与点P相同的速度沿射线CB方向运动,当点P到达点C时,两点运动同时停止,连接PQ交x轴于点G,作PE⊥x轴于点E,求EG的长.
(3)在(2)的条件下,以PQ为底边,在x轴的上方作等腰直角三角形,即PM=QM,∠M=90°,若△GCM的面积等于8,求点M的坐标.
(1)求m的值;
(2)动点P由点A出发沿AC向点C运动,同时点Q由点B出发,以与点P相同的速度沿射线CB方向运动,当点P到达点C时,两点运动同时停止,连接PQ交x轴于点G,作PE⊥x轴于点E,求EG的长.
(3)在(2)的条件下,以PQ为底边,在x轴的上方作等腰直角三角形,即PM=QM,∠M=90°,若△GCM的面积等于8,求点M的坐标.

▼优质解答
答案和解析
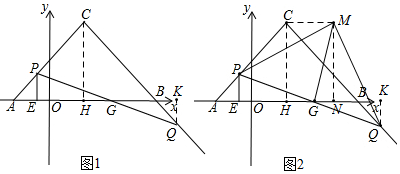 (1)如图1,作CH⊥AB于H,
(1)如图1,作CH⊥AB于H,
∵C(2,4),A(m-3,0),B(4m+2,0),
∴AH=2-(m-3)=5-m,BH=4m+2-2=4m,
∵AC=BC,
∴AH=KH,即5-m=4m,
解得m=1;
(2)如图1,作QK⊥x轴于K,
∵PE⊥AE,
∴∠BKQ=∠AEP=90°,
∵点Q由点B出发,以与点P相同的速度沿射线CB方向运动,
∴AP=BQ,
∵AC=BC,
∴∠CAB=∠CBA=∠KBQ
在△APE和△BQK中,
,
∴△APE≌△BQK(AAS),
∴PE=QK,AE=KB,
在△PEG和△QKG中,
,
∴△PEG≌△QKG(AAS),
∴EG=KG,
由(1)可得,m=1,
∴AO=2,BO=6,BK=AE=1,AB=2+6=8,
∴EG=
EK=
AB=4;
(3)如图2,作MN⊥y轴于N,连接CM,
∵△PEG≌△QKG,
∴PG=QG,
又∵PM=MQ,∠PMQ=90°,MG⊥PQ,
∴∠MQP=∠MPQ=∠GMQ=∠MQG=45°,
∴MG=GQ,
∵∠GMN+∠MGB=90°=∠QGK+∠MGK,
∴∠GMN=∠QGK,
在△MGN和△GQK中,
,
∴△MGN≌△GQK(AAS),
∴GK=MN,
又∵GK=EG=4,C(2,4),
∴MN=4=CH,
∴CM∥x轴,
∴∠MCH=∠CHE=90°,
∵△GCM的面积等于8,
∴
×CM×MN=8,即2CM=8,
∴CM=4,
∴矩形MNHC中,HN=CM=2,
又∵OH=2,
∴ON=OH+HN=2+4=6,
∴M(6,4).
 (1)如图1,作CH⊥AB于H,
(1)如图1,作CH⊥AB于H,∵C(2,4),A(m-3,0),B(4m+2,0),
∴AH=2-(m-3)=5-m,BH=4m+2-2=4m,
∵AC=BC,
∴AH=KH,即5-m=4m,
解得m=1;
(2)如图1,作QK⊥x轴于K,
∵PE⊥AE,
∴∠BKQ=∠AEP=90°,
∵点Q由点B出发,以与点P相同的速度沿射线CB方向运动,
∴AP=BQ,
∵AC=BC,
∴∠CAB=∠CBA=∠KBQ
在△APE和△BQK中,
|
∴△APE≌△BQK(AAS),
∴PE=QK,AE=KB,
在△PEG和△QKG中,
|
∴△PEG≌△QKG(AAS),
∴EG=KG,
由(1)可得,m=1,
∴AO=2,BO=6,BK=AE=1,AB=2+6=8,
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图2,作MN⊥y轴于N,连接CM,
∵△PEG≌△QKG,
∴PG=QG,
又∵PM=MQ,∠PMQ=90°,MG⊥PQ,
∴∠MQP=∠MPQ=∠GMQ=∠MQG=45°,
∴MG=GQ,
∵∠GMN+∠MGB=90°=∠QGK+∠MGK,
∴∠GMN=∠QGK,
在△MGN和△GQK中,
|
∴△MGN≌△GQK(AAS),
∴GK=MN,
又∵GK=EG=4,C(2,4),
∴MN=4=CH,
∴CM∥x轴,
∴∠MCH=∠CHE=90°,
∵△GCM的面积等于8,
∴
| 1 |
| 2 |
∴CM=4,
∴矩形MNHC中,HN=CM=2,
又∵OH=2,
∴ON=OH+HN=2+4=6,
∴M(6,4).
看了 如图,在平面直角坐标系中,已...的网友还看了以下:
在平面直角坐标系中,A(4,0),B(0,-4),C(0,4),点M为射线OA上A点右侧一动点在平 2020-05-13 …
已知椭圆C的中心在坐标原点O,焦点在x轴上,离心率为根号3/3,过其右焦点F的直线l的斜率为1时, 2020-05-16 …
设M={(x,y)|F(x,y)=0}为平面直角坐标系xOy内的点集,若对于任意(x1,y1)∈M 2020-06-14 …
已知点O(0,0)和点B(m,0)(m>0),动点P到O,B的距离比为2∶1,求P点轨迹和P点在什 2020-07-22 …
在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C为第一象限内一点,且AC 2020-07-30 …
如图,在平面直角坐标系中,直线AB交x轴于A(6,0),交y轴于B(0,6)P(m,n)是AB上一 2020-07-30 …
在平面直角坐标系xOy中,A(0,m)B(0,n)m>n>0.P为x轴正半轴上的一个动点,当∠AP 2020-07-30 …
在平面直角坐标系中,△ABC顶点坐标分别为A(0,0),B(1,3√),C(m,0)。若△ABC是 2020-07-30 …
如图所示,在竖直平面内有半径为R="0.2"m的光滑1/4圆弧AB,圆弧B处的切线水平,O点在B点 2020-07-31 …
在平面直角坐标系xOy中,椭圆C:=1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数), 2020-08-01 …