早教吧作业答案频道 -->数学-->
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.(1)求证:AP⊥BQ;(2)若AB=
题目详情
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
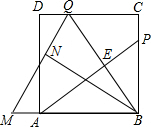
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.

(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠C=90°,AB=BC.
∴在△ABP和△BCQ中,
,
∴△ABP≌△BCQ,
∴∠BAP=∠CBQ.
∵∠BAP+∠APB=90°,
∴∠CBQ+∠APB=90°,
∴∠BEP=90°,
∴AP⊥BQ;
(2) ∵正方形ABCD中,AB=3,BP=2CP,
∴BP=2,
由(1)可得NQ=CQ=BP=2,NB=3.
又∵∠NQB=∠CQB=∠ABQ,
∴MQ=MB.
设MQ=MB=x,则MN=x-2.
在直角△MBN中,MB2=BN2+MN2,
即x2=32+(x-2)2,
解得:x=
,即MQ=
;
(3)∵BP=m,CP=n,
由(1)(2)得MQ=BM,CQ=QN=BP=m,
设AM=y,BN=BC=m+n,
在直角△BNM中,MB=y+m+n,MN=MQ-QN=(y+m+n)-m=y+n,
(y+m+n)2=(m+n)2+(y+n)2,
即y2+2(m+n)y+(m+n)2=(m+n)2+y2+2ny+n2,
则y=
,AM=
.
∴∠ABC=∠C=90°,AB=BC.
∴在△ABP和△BCQ中,
|
∴△ABP≌△BCQ,
∴∠BAP=∠CBQ.
∵∠BAP+∠APB=90°,
∴∠CBQ+∠APB=90°,
∴∠BEP=90°,
∴AP⊥BQ;
(2) ∵正方形ABCD中,AB=3,BP=2CP,
∴BP=2,
由(1)可得NQ=CQ=BP=2,NB=3.
又∵∠NQB=∠CQB=∠ABQ,
∴MQ=MB.
设MQ=MB=x,则MN=x-2.
在直角△MBN中,MB2=BN2+MN2,
即x2=32+(x-2)2,
解得:x=
| 13 |
| 4 |
| 13 |
| 4 |
(3)∵BP=m,CP=n,
由(1)(2)得MQ=BM,CQ=QN=BP=m,
设AM=y,BN=BC=m+n,
在直角△BNM中,MB=y+m+n,MN=MQ-QN=(y+m+n)-m=y+n,
(y+m+n)2=(m+n)2+(y+n)2,
即y2+2(m+n)y+(m+n)2=(m+n)2+y2+2ny+n2,
则y=
| n2 |
| 2m |
| n2 |
| 2m |
看了 如图,P为正方形ABCD的边...的网友还看了以下:
已知一次函数y=2x-4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴 2020-06-12 …
如图,已知点A(1,2)是反比例函数y=kx图象上的一点,连接AO并延长交双曲线的另一分支于点B, 2020-06-13 …
关于初三反比例函数:两个反比例函数y=k\x和y=1\x在第一象限的图像如图所示接上点P在y=k\ 2020-06-27 …
平行四边形ABCD中,AB=12,角B=45度,点P在边BC平行四边形ABCD中,AB=2cm,B 2020-07-20 …
P是△ABC内的一点,说明PA+PB+PC>1/2(AB+BC+AC)图为一个三边不相等三角形(三 2020-07-22 …
如图,直线l和双曲线y=k/x(k>0)交于A、B两点,p是线段AB上的一点(不与点A、B重合). 2020-07-26 …
如图,直线y=-x+6交x轴、y轴于A、B两点,p为A点右侧x轴上的一动点,以p为直角顶点、BP为 2020-07-26 …
如图,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,-3),顶点为点B,点P为抛物线 2020-07-26 …
(2014•武汉四月调考)在平面直角坐标系xOy中,抛物线c1:y=ax2-4a+4(a<0)经过 2020-07-31 …
(2014•龙岩模拟)设A是圆x2+y2=1上的动点,点A在x轴上的投影为B,点P在AB上,记点P的 2020-11-02 …