早教吧作业答案频道 -->数学-->
如图,在△BCE中,点A是边BE上一点,以AB为直径的O与CE相切于点D,AD∥OC,点F为OC与O的交点,连接AF.(1)求证:CB是O的切线;(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
题目详情
如图,在△BCE中,点A是边BE上一点,以AB为直径的 O与CE相切于点D,AD∥OC,点F为OC与 O的交点,连接AF.
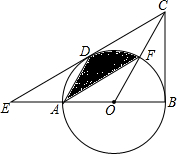
(1)求证:CB是 O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

(1)求证:CB是 O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
▼优质解答
答案和解析
(1)证明:连接OD,与AF相交于点G,
∵CE与 O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠1,∠DAO=∠2,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠1=∠2,
在△CDO和△CBO中,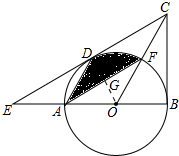
,
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是 O的切线.
(2)由(1)可知∠3=∠BCO,∠1=∠2,
∵∠ECB=60°,
∴∠3=
∠ECB=30°,
∴∠1=∠2=60°,
∴∠4=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠1=∠ADO,
在△ADG和△FOG中,
,
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴ O的半径r=3,
∴S阴=S扇形ODF=
=
π.
∵CE与 O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠1,∠DAO=∠2,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠1=∠2,
在△CDO和△CBO中,

|
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是 O的切线.
(2)由(1)可知∠3=∠BCO,∠1=∠2,
∵∠ECB=60°,
∴∠3=
| 1 |
| 2 |
∴∠1=∠2=60°,
∴∠4=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠1=∠ADO,
在△ADG和△FOG中,
|
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴ O的半径r=3,
∴S阴=S扇形ODF=
| 60π•32 |
| 360 |
| 3 |
| 2 |
看了 如图,在△BCE中,点A是边...的网友还看了以下:
如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针 2020-05-14 …
1/4x^2+y^2=1,有直线y=kx+4过椭圆交于A,B点,O为中心,若OA与OB斜率之和为4 2020-05-19 …
过点A(-2,0)的直线y=kx+b与y轴交于点B,点O为坐标原点,若△OAB的面积≤3,求k的取 2020-06-06 …
过点a(-2,0)的直线y=kx+b与y轴交于点b,点o为坐标原点,若△abo的面积≤2,求k的取 2020-06-06 …
过点A(-2,0)的直线y=kx+b与y轴交于点B,点O为坐标原点,弱S▷AOB≤2,则K的取值范 2020-06-06 …
如图所示,在两等量异种点电荷的电场中,O点为两电荷连线上的中点,MN为两电荷连线的中垂线.a、b、 2020-08-01 …
(2033•江门模拟)读经纬网l回答3-2题1.对给出A(120°E,40°N),中(30°W,40 2020-11-12 …
1已知一次函数y=k(x+m)+b经过A(1,2),B(2,-1)两点,则此函数解析式为()它与x轴 2020-11-27 …
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是()A.DE是△ABC的中 2020-12-24 …
(2008•延庆县二模)如图所示,边长为2的等边三角形OBA的顶点A在x轴的正半轴上,B点位于第一象 2021-02-04 …