早教吧作业答案频道 -->数学-->
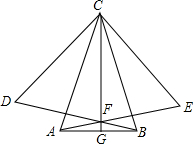
如图,等腰△ABC中,AC=BC,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:G为AB的中点.
题目详情
如图,等腰△ABC中,AC=BC,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:G为AB的中点.

▼优质解答
答案和解析
证明:∵CA=CB
∴∠CAB=∠CBA
∵△AEC和△BCD为等边三角形
∴∠CAE=∠CBD,∠FAG=∠FBG
∴AF=BF.
在三角形ACF和△CBF中,
,
∴△AFC≌△BCF(SSS),
∴∠ACF=∠BCF
∴AG=BG(三线合一)
∴G为AB的中点
∴∠CAB=∠CBA
∵△AEC和△BCD为等边三角形
∴∠CAE=∠CBD,∠FAG=∠FBG
∴AF=BF.
在三角形ACF和△CBF中,
|
∴△AFC≌△BCF(SSS),
∴∠ACF=∠BCF
∴AG=BG(三线合一)
∴G为AB的中点
看了 如图,等腰△ABC中,AC=...的网友还看了以下:
四边形ABCD是平行四边形,E是对角线AC上一点,射线DE分别交射线CB、AB于点F、G.(1)如 2020-06-12 …
有关二阶导的问题设f(x),g(x)在点a处可导,且f(a)=g(b)=0,f'(a)*g'(a) 2020-06-18 …
如图,边长为6cm的正方形ABCD中,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时 2020-06-21 …
分别做出一个函数f(x),g(x)满足:f(x),g(x)定义域为实数集R,f(x)在任意点不可导 2020-06-25 …
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、A 2020-07-09 …
(2010•芜湖)芜湖国际动漫节期间,小明进行了富有创意的形象设计.如图1,他在边长为1的正方形A 2020-07-15 …
如图长方形ABCD的边AD=8cm,AB=6cm,E为AD中点,对角线AC、BD交于O点.BE、C 2020-07-30 …
如图,两只小虫甲和乙,沿长方形ABCD的边按箭头方向爬行,在离C点32厘米的E点第一次相遇,后两次相 2020-12-14 …
请问这题怎么做:设函数f(x)与g(x)在点x.连续,证明函数t(x)=max{f(x),g(x)} 2021-01-11 …
小芳参加图书馆标志设计大赛,他在边长为2的正方形ABCD内作等边△BCE,并与正方形的对角线交于F、 2021-01-15 …