早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,一次函数的图象与x轴、y轴分别交于A(3,0)、B(0,3).(1)求一次函数的解析式:(2)若点P在该函数图象上,P到x轴、y轴的距离分别为d1,d2,求d1-d2的取值范
题目详情
在平面直角坐标系xOy中,一次函数的图象与x轴、y轴分别交于A(3,0)、B(0,3).
(1)求一次函数的解析式:
(2)若点P在该函数图象上,P到x轴、y轴的距离分别为d1,d2,求d1-d2的取值范围;
(3)在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴上的顶点坐标.
(1)求一次函数的解析式:
(2)若点P在该函数图象上,P到x轴、y轴的距离分别为d1,d2,求d1-d2的取值范围;
(3)在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴上的顶点坐标.

▼优质解答
答案和解析
(1)设直线AB的解析式为y=kx+b,
将点A(3,0)、B(0,3)代入y=kx+b中,
得:
,解得:
,
∴直线AB的解析式为y=-x+3.
(2)设点P的坐标为(m,-m+3),
∴d1=|m|,d2=|-m+3|,
∴d1-d2=|m|-|-m+3|.
当m<0时,-m+3>0,
d1-d2=|m|-|-m+3|=-m-(-m+3)=3;
当0≤m≤3时,-m+3≥0,
d1-d2=|m|-|-m+3|=m-(-m+3)=2m-3,
∵0≤m≤3,
∴-3≤d1-d2≤3;
当3<m时,-m+3<0,
d1-d2=|m|-|-m+3|=m-(m-3)=3.
综上可知:当点P在该函数图象上时,P到x轴、y轴的距离分别为d1,d2,则d1-d2的取值范围为-3≤d1-d2≤3.
(3)分两种情况: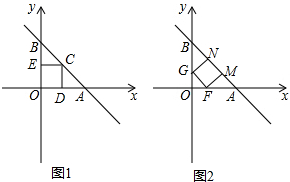
①如图1,当点O为正方形的一个顶点时,
∵OA=OB,
∴∠BAO=45°,
∵CD⊥OA,
∴CD=AD.
∵四边形ODCE是正方形,
∴OD=CD,
∴OD=AD,
∴OD=
OA=
,
∴落在x轴上的顶点(0,0),(
,0);
②如图2,当正方形的两个顶点落在线段AB上时,
∵∠BAO=∠ABO=45°,
∴△AFE和△BGN均为等腰直角三角形,
∴BN=GN,AM=FM,
∵四边形FMNG为正方形,
∴AM=MN=BN,
∴AM=
AB=
=
,AF=
=2.
∵OA=3,
∴OF=3-2=1,
∴落在x轴上的顶点F(1,0).
综上可知:正方形落在x轴上的顶点坐标为(0,0)、(
,0)和(1,0).
将点A(3,0)、B(0,3)代入y=kx+b中,
得:
|
|
∴直线AB的解析式为y=-x+3.
(2)设点P的坐标为(m,-m+3),
∴d1=|m|,d2=|-m+3|,
∴d1-d2=|m|-|-m+3|.
当m<0时,-m+3>0,
d1-d2=|m|-|-m+3|=-m-(-m+3)=3;
当0≤m≤3时,-m+3≥0,
d1-d2=|m|-|-m+3|=m-(-m+3)=2m-3,
∵0≤m≤3,
∴-3≤d1-d2≤3;
当3<m时,-m+3<0,
d1-d2=|m|-|-m+3|=m-(m-3)=3.
综上可知:当点P在该函数图象上时,P到x轴、y轴的距离分别为d1,d2,则d1-d2的取值范围为-3≤d1-d2≤3.
(3)分两种情况:

①如图1,当点O为正方形的一个顶点时,
∵OA=OB,
∴∠BAO=45°,
∵CD⊥OA,
∴CD=AD.
∵四边形ODCE是正方形,
∴OD=CD,
∴OD=AD,
∴OD=
| 1 |
| 2 |
| 3 |
| 2 |
∴落在x轴上的顶点(0,0),(
| 3 |
| 2 |
②如图2,当正方形的两个顶点落在线段AB上时,
∵∠BAO=∠ABO=45°,
∴△AFE和△BGN均为等腰直角三角形,
∴BN=GN,AM=FM,
∵四边形FMNG为正方形,
∴AM=MN=BN,
∴AM=
| 1 |
| 3 |
| 1 |
| 3 |
| 32+32 |
| 2 |
| 2+2 |
∵OA=3,
∴OF=3-2=1,
∴落在x轴上的顶点F(1,0).
综上可知:正方形落在x轴上的顶点坐标为(0,0)、(
| 3 |
| 2 |
看了 在平面直角坐标系xOy中,一...的网友还看了以下:
根据下面给出的数轴,解答下面的问题:⑴请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: 2020-05-13 …
关于轴对称图形的问题关于轴对称图形的一些问题,解答标明题号1.轴对称图形,有几条对称轴,是只有一条 2020-05-16 …
已知函数f(x)=3sinωx(A>0,ω>0)的部分图象如图所示.P、Q分别是图象上的一个最高点 2020-06-13 …
已知直线y=-4分之3x+6的图像交x轴与点A,交y轴于点B,在线段OA上找一点E,将△ABE沿着 2020-06-14 …
直观图中Y轴理解都知道Y轴线段长度只能画一半可是有点迷茫为啥就画一半人的视角看到的到底是什么?而画 2020-06-27 …
根据下面给出的数轴,解答下面的问题:(1)请你根据图中A、B(在-2,-3的正中间)两点的位置,分 2020-07-30 …
质点相对于轴的角动量L=rp期中,r,p分别代表什么?还有力相对于轴的力矩m=rf的物理量又分别代表 2020-11-05 …
根据下面给出的数轴,解答下面的问题:(1)请你根据图中A、B(在-3,-2的正中间)两点的位置,分别 2020-11-23 …
如图,有四列简谐波同时沿x轴正方向传播,波速分别是v、2v、3v和4v,a、b是x轴上所给定的两点, 2020-12-09 …
用matlab编程解决这道题目。希望有详细的解答过程和图解。若0≤x≤2π,试在不同子图内分别绘制曲 2021-01-15 …