早教吧作业答案频道 -->数学-->
定义:既有外接圆,又有内切圆的凸多边形叫做双圆多边形.如图1,O1是△ABC外接圆,O2是△ABC的内切圆,则△ABC就是双圆三角形.(1)请写出一个双圆四边形的名你;(2)如图2,已知
题目详情
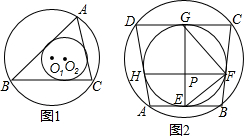
定义:既有外接圆,又有内切圆的凸多边形叫做双圆多边形.如图1, O1是△ABC外接圆, O2是△ABC的内切圆,则△ABC就是双圆三角形.
(1)请写出一个双圆四边形的名你___;
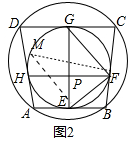
(2)如图2,已知四边形ABCD是双圆四边形,其内切圆与四条边相切于点E,F,G,H,且EG是内切圆的直径,交弦FH于点P,连接EF,FG.
①当∠FGE=40°时,求∠BFE的度数;
②求证:HF⊥GE.
(1)请写出一个双圆四边形的名你___;
(2)如图2,已知四边形ABCD是双圆四边形,其内切圆与四条边相切于点E,F,G,H,且EG是内切圆的直径,交弦FH于点P,连接EF,FG.
①当∠FGE=40°时,求∠BFE的度数;
②求证:HF⊥GE.

▼优质解答
答案和解析
(1)正方形既有外接圆,又有内切圆,所以正方形是双圆四边形,
故答案为正方形.
(2)①如图2中,作直径FM,连接EM,
∵FM是直径,
∴∠MEF=90°,
∴∠EMF+∠MFE=90°,
∵BF是切线,
∴MF⊥BF,
∴∠MFB=90°,
∴∠MFE+∠EFB=90°,
∴∠EMF=∠EFB,
∵∠EMF=∠EGF,
∴∠EFB=∠EGF=40°.
②如图3中,连接HG.
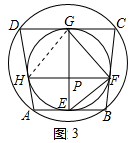
∵四边形ABCD是圆内接四边形,
∴∠D+∠B=180°,
∵H、G、F、E是切点,
∴DG=DH,BF=BE,
∴∠DHG=∠DGH,∠BEF=∠BFE,
∴∠D+2∠DGH=180°,∠B+2∠EFB=180°,
∴2∠DGH+2∠EFB=180°,
∴∠DGH+∠EFB=90°,
由①可知,∠EFB=∠EGF,∠DGH=∠HFG,
∴∠EGF+∠HFG=90°,
∴∠GPE=90°,
∴HF⊥GE.
故答案为正方形.
(2)①如图2中,作直径FM,连接EM,

∵FM是直径,
∴∠MEF=90°,
∴∠EMF+∠MFE=90°,
∵BF是切线,
∴MF⊥BF,
∴∠MFB=90°,
∴∠MFE+∠EFB=90°,
∴∠EMF=∠EFB,
∵∠EMF=∠EGF,
∴∠EFB=∠EGF=40°.
②如图3中,连接HG.

∵四边形ABCD是圆内接四边形,
∴∠D+∠B=180°,
∵H、G、F、E是切点,
∴DG=DH,BF=BE,
∴∠DHG=∠DGH,∠BEF=∠BFE,
∴∠D+2∠DGH=180°,∠B+2∠EFB=180°,
∴2∠DGH+2∠EFB=180°,
∴∠DGH+∠EFB=90°,
由①可知,∠EFB=∠EGF,∠DGH=∠HFG,
∴∠EGF+∠HFG=90°,
∴∠GPE=90°,
∴HF⊥GE.
看了 定义:既有外接圆,又有内切圆...的网友还看了以下:
边缘粗糙,半径不同的两个轮子,作无滑动的摩擦传动.AB是大轮O上的两点,OA=R=0.8m,OB= 2020-05-13 …
(3)若只将钩码的悬挂点由A移至C,O、B位置不变,仍将钩码提升相同的高度,则杠杆的机械效率将(选 2020-06-20 …
水平放置的△ABC的直观图如图,其中B′O′=C′O′=1,A′O′=32,那么原△ABC是一个( 2020-06-27 …
一道初二数学选择题!下列说法正确的是()A.无限小数都是无理数B.无理数是无限小数C.邻边相等的四 2020-06-27 …
等边三角形OBC的边长为10,点p沿O→B→C→O的方向运动等边三角形OBC的边长为10,点P沿O 2020-07-22 …
平行四边形ABCO四个定点坐标分别是A(√3,√3)B(3√3,√3)C(2√3,0)O(0,0) 2020-07-30 …
已知三角形ABC的三边长BC=a,AC=b,AB=c,O为ABC所在平面内一点,若aOA已知三角形 2020-08-01 …
把△ABC按斜二测画法得到△A′B′C′(如图所示),其中B′O′=C′O′=1,A′O′=32, 2020-08-02 …
已知:如图,在平面直角坐标系中.四边形ABCO是长方形,∠OAB=∠B=∠BCO=90°,AB∥CO 2020-11-01 …
三角形内心推导(高三)三角形ABC的边长分别为a,b,c,O是平面ABC上的点,若a*OA+b*OB 2021-01-19 …