若函数f(x)=lg(|x|-1)，|x|>1asin(π2x)，|x|≤1，关于x的方程f2（x）-（a+1）f（x）+a=0，给出下列结论：①存在这样的实数a，使得方程由3个不同的实根；②不存在这样的实数a，使得方程由4个不同

Question

若函数f(x)=

lg(|x|-1)，|x|>1

asin((π)/(2)x)，|x|≤1

，关于x的方程f²（x）-（a+1）f（x）+a=0，给出下列结论：
①存在这样的实数a，使得方程由3个不同的实根；
②不存在这样的实数a，使得方程由4个不同的实根；
③存在这样的实数a，使得方程由5个不同的实数根；
④不存在这样的实数a，使得方程由6个不同的实数根．
其中正确的个数是（　　）

A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

∵f²（x）-（a+1）f（x）+a=0，
∴f（x）=1或f（x）=a，
作函数f(x)=

lg(|x|-1)，|x|>1

asin((π)/(2)x)，|x|≤1

的图象如下，
，
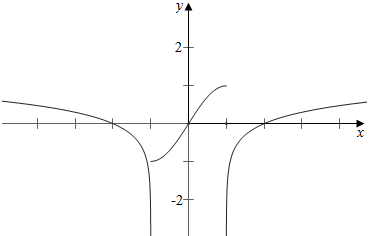当a=1时，方程有3个不同的实根，故①正确；
当a>1或a≤-1时，方程有6个不同的实根，故④不正确；
当-1<a<1时，方程有5个不同的实根，故③正确；
综上可知，
不存在这样的实数a，使得方程由4个不同的实根；故②正确；
故选：C．