已知函数f(x)=e|x-1|，x>0-x2-2x+1，x≤0，若关于x的方程f2（x）-3f（x）+a=0（a∈R）有8个不等的实数根，则a的取值范围是（）A.(0，14)B.(13，3)C.（1，2）D.(2，94)

Question

已知函数f(x)=

e|x-1|  ， x>0

-x2-2x+1 ，x≤0

，若关于x的方程f²（x）-3f（x）+a=0（a∈R）有8个不等的实数根，则a的取值范围是（　　）

A. (0，

(1)/(4))

B. (

(1)/(3)，3)

C. （1，2）

D. (2，

(9)/(4))

Answer 1

函数f(x)=

e|x-1|  ， x>0

-x2-2x+1 ，x≤0

，的图象如图：
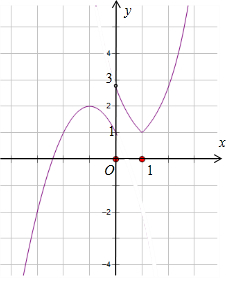
关于x的方程f²（x）-3f（x）+a=0（a∈R）有8个不等的实数根，f（x）必须有两个不相等的实数根，由函数f（x）图象
可知f（x）∈（1，2）．令t=f（x），
方程f²（x）-3f（x）+a=0化为：a=-t²+3t，t∈（1，2），
a=-t²+3t，开口向下，对称轴为：t=(3)/(2)，
可知：a的最大值为：-（(3)/(2)）²+3×(3)/(2)=(9)/(4)，
a的最小值为：2．
a∈（2，(9)/(4)]．
故选：D．