早教吧作业答案频道 -->数学-->
如图,已知抛物线y=-x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).(1)求抛物线的函数表达
题目详情
如图,已知抛物线y=-x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).
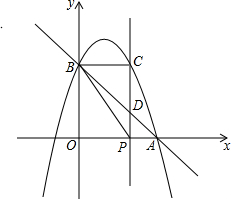
(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为___.(直接写出答案)

(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为___.(直接写出答案)
▼优质解答
答案和解析
(1)∵抛物线y=-x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),
∴-9+3b+c=0,c=3,
∴b=2,
∴抛物线解析式为y=-x2+2x+3;
(2)∵A(3,0),B(0,3),∴直线AB解析式为y=-x+3,
∵P(x,0).
∴D(x,-x+3),C(x,-x2+2x+3),
∵0∴CD=-x2+2x+3-(-x+3)=-x2+3x=-(x-
)2+
,
当x=
时,CD最大=
;
(3)由(2)知,CD=|-x2+3x|,DP=|-x+3|
①当S△PDB=2S△CDB时,
∴PD=2CD,
即:2|-x2+3x|=|-x+3|,
∴x=±
或x=3(舍),
②当2S△PDB=S△CDB时,
∴2PD=CD,
即:|-x2+3x|=2|-x+3|,
∴x=±2或x=3(舍),
即:综上所述,x=±
或x=±2;
(4)直线AB解析式为y=-x+3,
∴线段AB的垂直平分线l的解析式为y=x,
∵过点B,C,P的外接圆恰好经过点A,
∴过点B,C,P的外接圆的圆心既是线段AB的垂直平分线上,也在线段PC的垂直平分线上,
∴
=x,
∴x=±
,
故答案为:±
∴-9+3b+c=0,c=3,
∴b=2,
∴抛物线解析式为y=-x2+2x+3;
(2)∵A(3,0),B(0,3),∴直线AB解析式为y=-x+3,
∵P(x,0).
∴D(x,-x+3),C(x,-x2+2x+3),
∵0
| 3 |
| 2 |
| 9 |
| 4 |
当x=
| 3 |
| 2 |
| 9 |
| 4 |
(3)由(2)知,CD=|-x2+3x|,DP=|-x+3|
①当S△PDB=2S△CDB时,
∴PD=2CD,
即:2|-x2+3x|=|-x+3|,
∴x=±
| 1 |
| 2 |
②当2S△PDB=S△CDB时,
∴2PD=CD,
即:|-x2+3x|=2|-x+3|,
∴x=±2或x=3(舍),
即:综上所述,x=±
| 1 |
| 2 |
(4)直线AB解析式为y=-x+3,
∴线段AB的垂直平分线l的解析式为y=x,
∵过点B,C,P的外接圆恰好经过点A,
∴过点B,C,P的外接圆的圆心既是线段AB的垂直平分线上,也在线段PC的垂直平分线上,
∴
| -x2+2x+3 |
| 2 |
∴x=±
| 3 |
故答案为:±
| 3 |
看了 如图,已知抛物线y=-x2+...的网友还看了以下:
如图,已知二次函数y=x+bx+c过点A(1,0)(1)求此二次函数的解析式(2)在抛物线上如图, 2020-04-26 …
25、如图,已知抛物线 y=-x2+bx+c过点A(2,0),对称轴为y轴,顶点为P. (1)求该 2020-05-16 …
点M(4,0)以点M为圆心、2为半径的圆与x轴交与点A,B,已知抛物线y=1/6x^2+bx+c过 2020-05-16 …
一道傻傻的物理光学选择题(一-39)已知物点A、像点B的位置及透镜的主光轴MN,则下列关于作光路图 2020-05-22 …
如图,抛物线y=ax²+bx+c(a>0交x轴于A,B两点,交y轴于C点,A点在B点的左侧,已知B 2020-06-14 …
如果抛物线y=ax2+bx+c,过定点M(1,1),则称此抛物线为定点抛物线.(1)请你写出一条定 2020-07-01 …
已知O点为坐标原点,抛物线y1=ax2+bx+c(a≠0)与y轴交于点C,且O,C两点间的距离为3. 2020-11-01 …
已知抛物线y=x方+bx+3a,过点A(1,0)B(0,-3)与x轴交于另一点c.已知抛物线y=x方 2020-11-27 …
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是 2020-12-23 …
已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动 2021-01-12 …