早教吧作业答案频道 -->数学-->
已知,在以O为原点的直角坐标系中,抛物线的顶点为A(-1,-4),且经过点B(-2,-3),与x轴分别交于C、D两点.(1)求直线OB以及该抛物线相应的函数表达式;(2)如图1,点M是抛物线上
题目详情
已知,在以O为原点的直角坐标系中,抛物线的顶点为A (-1,-4),且经过点B(-2,-3),与x轴分别交于C、D两点.
(1)求直线OB以及该抛物线相应的函数表达式;
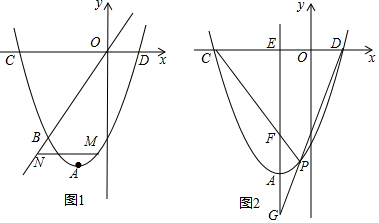
(2)如图1,点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB交于点N,求MN的最大值;
(3)如图2,过点A的直线交x轴于点E,且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.

(1)求直线OB以及该抛物线相应的函数表达式;
(2)如图1,点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB交于点N,求MN的最大值;
(3)如图2,过点A的直线交x轴于点E,且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
▼优质解答
答案和解析
(1)设直线OB解析式为y=kx,由题意可得-3=-2k,解得k=
,
∴直线OB解析式为y=
x,
∵抛物线顶点坐标为(-1,-4),
∴可设抛物线解析式为y=a(x+1)2-4,
∵抛物线经过B(-2,-3),
∴-3=a-4,解得a=1,
∴抛物线为y=x2+2x-3;
(2)设M(t,t2+2t-3),MN=s,则N的横坐标为t-s,纵坐标为
(t-s),
∵MN∥x轴,
∴t2+2t-3=
(t-s),得s=-
t2-
t+2=-
(t+
)2+
,
∴当t=-
时,MN有最大值,最大值为
;
(3)EF+EG=8.
理由如下:
如图2,过点P作PQ∥y轴交x轴于Q,
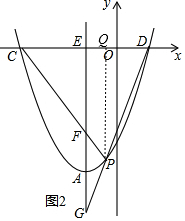
在y=x2+2x-3中,令y=0可得0=x2+2x-3,解得x=-3或x=1,
∴C(-3,0),D(1,0),
设P(t,t2+2t-3),则PQ=-t2-2t+3,CQ=t+3,DQ=1-t,
∵PQ∥EF,
∴△CEF∽△CQP,
∴
=
,
∴EF=
•PQ=
(-t2-2t+3),
同理△EGD∽△QPD得
=
,
∴EG=
•PQ=
•(-t2-2t+3),
∴EF+EG=
(-t2-2t+3)+
•(-t2-2t+3)=2(-t2-2t+3)(
+
)=2(-t2-2t+3)(
)=2(-t2-2t+3)(
)=8,
∴当点P运动时,EF+EG为定值8.
(1)设直线OB解析式为y=kx,由题意可得-3=-2k,解得k=
| 3 |
| 2 |
∴直线OB解析式为y=
| 3 |
| 2 |
∵抛物线顶点坐标为(-1,-4),
∴可设抛物线解析式为y=a(x+1)2-4,
∵抛物线经过B(-2,-3),
∴-3=a-4,解得a=1,
∴抛物线为y=x2+2x-3;
(2)设M(t,t2+2t-3),MN=s,则N的横坐标为t-s,纵坐标为
| 3 |
| 2 |
∵MN∥x轴,
∴t2+2t-3=
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 49 |
| 24 |
∴当t=-
| 1 |
| 4 |
| 49 |
| 24 |
(3)EF+EG=8.
理由如下:
如图2,过点P作PQ∥y轴交x轴于Q,

在y=x2+2x-3中,令y=0可得0=x2+2x-3,解得x=-3或x=1,
∴C(-3,0),D(1,0),
设P(t,t2+2t-3),则PQ=-t2-2t+3,CQ=t+3,DQ=1-t,
∵PQ∥EF,
∴△CEF∽△CQP,
∴
| EF |
| PQ |
| CE |
| CQ |
∴EF=
| CE |
| CQ |
| 2 |
| t+3 |
同理△EGD∽△QPD得
| EG |
| PQ |
| DE |
| DQ |
∴EG=
| DE |
| DQ |
| 2 |
| 1-t |
∴EF+EG=
| 2 |
| t+3 |
| 2 |
| 1-t |
| 1 |
| t+3 |
| 1 |
| 1-t |
| 1-t+t+3 |
| (t+3)(1-t) |
| 4 |
| -t2-2t+3 |
∴当点P运动时,EF+EG为定值8.
看了 已知,在以O为原点的直角坐标...的网友还看了以下:
已知圆O方程为x^2+(y-1)^2=5,直线L方程Mx-y+1-M=0(1)求证当M∈R时,L与 2020-05-23 …
中考变试题.如图,在菱形abcd中,对角线ac,bd交于o,与ob为直径画圆m如图,在菱形abcd 2020-06-23 …
已知圆M的方程为:x²+y²-2x-2y-6=0,以坐标原点为圆心的圆O与圆M相切已知圆M的方程为 2020-06-27 …
已知抛物线y=(x-b)2+m-b的顶点为m与轴交于点A(x1,O),B(x2,O),且△MAB为 2020-07-12 …
(2000•江西)如图,已知O是正方形ABCD对角线AC上一点,以O为圆心、OA的长为半径的⊙O与 2020-07-20 …
如图,O为正方形ABCD对角线上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.(1)求证: 2020-07-30 …
已知圆O:x2+y2=4,点P是直线X=4上的动点,若点A(-2,0),B(2,0),直线PA,P 2020-07-30 …
在平面直角坐标系xOy中,半径为1的O与x轴负半轴交于点A,点M在O上,将点M绕点A顺时针旋转60° 2020-11-01 …
已知⊙O与⊙O′内切于点A,⊙O的弦BC与⊙O′切于点D,AB、AC与⊙O′分别交于点E、F,AG、 2020-12-01 …
已知A为⊙O上一点,B为⊙A与OA的交点,⊙A与⊙O的半径分别为r、R,且r<R.(Ⅰ)如图1,过点 2021-01-11 …