早教吧作业答案频道 -->数学-->
如图,过点C(4,3)的抛物线的顶点为M(2,-1),交x轴于A、B两点(点A在点B的左侧),交y轴于点D.(1)求抛物线的解析式及点D的坐标;(2)点P是抛物线对称轴上的一个动点,求使△PBC
题目详情
如图,过点C(4,3)的抛物线的顶点为M(2,-1),交x轴于A、B两点(点A在点B的左侧),交y轴于点D.
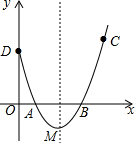
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一个动点,求使△PBC为直角三角形的点P坐标;
(3)若点Q在第一象限内,且tan∠AQB=2,线段DQ是否存在最小值,如果存在直接写出最小值;如果不存在,请说明理由.

(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一个动点,求使△PBC为直角三角形的点P坐标;
(3)若点Q在第一象限内,且tan∠AQB=2,线段DQ是否存在最小值,如果存在直接写出最小值;如果不存在,请说明理由.
▼优质解答
答案和解析
(1)∵抛物线的顶点为M(2,-1),
∴设抛物线解析式为y=a(x-2)2-1,
∵抛物线过点C(4,3),
∴3=a×4-1,
∴a=1,
∴抛物线的解析式为y=(x-2)2-1=x2-4x+3,
∵抛物线交y轴于点D,
∴点D(0,3),
(2)由(1)得,抛物线的解析式为y=(x-2)2-1,
∴抛物线的对称轴为x=2,
设点P(2,m),
∵抛物线交x轴于A、B两点,
∴A(1,0),B(3,0),
∴PB2=1+m2,PC2=4+(m-3)2,BC2=12+32=10,
∵△PBC为直角三角形,
①当∠CPB=90°时,
∴PB2+PC2=BC2,
∴1+m2+(m-3)2=10,
∴m1=1,m2=2,
∴P(2,1),或P(2,2),
②当∠PBC=90°时,
∴PB2+BC2=PC2,
∴10+1+m2=4+(m-3)2,
∴m=
,
∴P(2,
),
③当∠PCB=90°时,
∴PB2=BC2+PC2,
∴1+m2=4+(m-3)2+10,
∴m=
,
∴P(2,
),
∴使△PBC为直角三角形的点P坐标P(2,1)或P(2,2)或P(2,
)或P(2,
);
(3)如图,
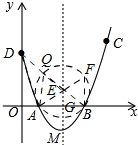
由(2)有,A(1,0),B(3,0),
∴AB=2,
过点B作BF⊥AB,截取BF=
AB=1,
连接AF,
∴根据勾股定理得,AF=
,
以AF为直径作圆,圆心为点E,则点E在抛物线的对称轴上,
∴EG=
BF=
,
∴点E(2,
),
∵∠AQB=∠AFB,
连接DE,交 E于Q,所以此时线段DQ最小,
∵D(0,3),
∴DE=
=
,
∴DQ=DE-QE=DE-
AF=
∴设抛物线解析式为y=a(x-2)2-1,
∵抛物线过点C(4,3),
∴3=a×4-1,
∴a=1,
∴抛物线的解析式为y=(x-2)2-1=x2-4x+3,
∵抛物线交y轴于点D,
∴点D(0,3),
(2)由(1)得,抛物线的解析式为y=(x-2)2-1,
∴抛物线的对称轴为x=2,
设点P(2,m),
∵抛物线交x轴于A、B两点,
∴A(1,0),B(3,0),
∴PB2=1+m2,PC2=4+(m-3)2,BC2=12+32=10,
∵△PBC为直角三角形,
①当∠CPB=90°时,
∴PB2+PC2=BC2,
∴1+m2+(m-3)2=10,
∴m1=1,m2=2,
∴P(2,1),或P(2,2),
②当∠PBC=90°时,
∴PB2+BC2=PC2,
∴10+1+m2=4+(m-3)2,
∴m=
| 1 |
| 3 |
∴P(2,
| 1 |
| 3 |
③当∠PCB=90°时,
∴PB2=BC2+PC2,
∴1+m2=4+(m-3)2+10,
∴m=
| 11 |
| 3 |
∴P(2,
| 11 |
| 3 |
∴使△PBC为直角三角形的点P坐标P(2,1)或P(2,2)或P(2,
| 1 |
| 3 |
| 11 |
| 3 |
(3)如图,

由(2)有,A(1,0),B(3,0),
∴AB=2,
过点B作BF⊥AB,截取BF=
| 1 |
| 2 |
连接AF,
∴根据勾股定理得,AF=
| 5 |
以AF为直径作圆,圆心为点E,则点E在抛物线的对称轴上,
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
∴点E(2,
| 1 |
| 2 |
∵∠AQB=∠AFB,
连接DE,交 E于Q,所以此时线段DQ最小,
∵D(0,3),
∴DE=
22+(
|
| ||
| 2 |
∴DQ=DE-QE=DE-
| 1 |
| 2 |
|
看了 如图,过点C(4,3)的抛物...的网友还看了以下:
1.一直一条抛物线的开口方向和形状大小与抛物线y=3x^2都相同,顶点在抛物线y=(x+2)^2的 2020-05-13 …
如图,抛物线y=-x^2+bx+c经过点A(1,0)和点B(0,5).(1)求此抛物线的解析式及顶 2020-05-16 …
已知二次函数的图象经过A(2,0)、C(0,12)两点,且对称轴为直线x=4,设顶点为点P,与x轴 2020-05-17 …
如图1,已知抛物线y=-x2+bx+c经过点A(1,0)和点B(-3,0),该抛物线与y轴的交点为 2020-05-17 …
已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x-h)2的顶点为P(1,0) 2020-06-14 …
阅读下列材料:当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生 2020-06-14 …
抛物线y=ax2+bx(a≠0)经过点A(1,94),对称轴是直线x=2,顶点是D,与x轴正半轴的 2020-07-21 …
已知平面直角坐标系中两定点A(-1,0)、B(4,0),抛物线y=ax2+bx-2(a≠0)过点A 2020-07-26 …
直线l经过A(4,0),B(0,4)两点,抛物线y=a(x-h)2的顶点为P(1,0),与抛物线的 2020-07-26 …
二次函数超基础问题,求救1.二次函数解析式的一般式(通式):化为顶点为:其中二次项系数是A,一次向系 2020-11-07 …
 扫描下载二维码
扫描下载二维码
