早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,把抛物线C1:y=x2-4沿x轴向右平移m(m>0)个单位长度,得抛物线C2,C1和C2的交点为点M(如图1)(1)用含m的式子来表示抛物线C2的解析式和点M的坐标;(2)定义:
题目详情
在平面直角坐标系xOy中,把抛物线C1:y=x2-4沿x轴向右平移m(m>0)个单位长度,得抛物线C2,C1和C2的交点为点M(如图1)
(1)用含m的式子来表示抛物线C2的解析式和点M的坐标;
(2)定义:像C1和C2两条抛物线,是把其中一条沿水平方向向左(像向右)平移得到另一条.若两抛物线的顶点P、Q以及交点M满足∠PMQ=90°,则这样的两条抛物线互为“和谐线”.
①求抛物线C1:y=x2-4的和谐线;
②如图2,抛物线C1:y=x2-4与x轴正半轴的交点为A,与它的和谐线的交点为M(点M在第四象限),连接MA,过点M作MH⊥x轴,在x轴上存在一点N,使∠ONM+∠AMH=45°,求点N的坐标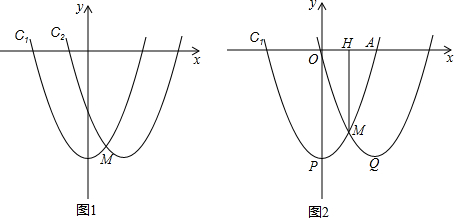
(1)用含m的式子来表示抛物线C2的解析式和点M的坐标;
(2)定义:像C1和C2两条抛物线,是把其中一条沿水平方向向左(像向右)平移得到另一条.若两抛物线的顶点P、Q以及交点M满足∠PMQ=90°,则这样的两条抛物线互为“和谐线”.
①求抛物线C1:y=x2-4的和谐线;
②如图2,抛物线C1:y=x2-4与x轴正半轴的交点为A,与它的和谐线的交点为M(点M在第四象限),连接MA,过点M作MH⊥x轴,在x轴上存在一点N,使∠ONM+∠AMH=45°,求点N的坐标

▼优质解答
答案和解析
(1)∵抛物线C1:y=x2-4①沿x轴向右平移m(m>0)个单位长度,得抛物线C2,
∴抛物线C2的解析式为y=(x-m)2-4=x2-2mx+m2-4②,
联立①②得,x=
,y=
-4,
∴M(
,
-4);
(2)设抛物线C1:y=x2-4的和谐线抛物线C2的解析式为y=(x-m)2-4,
∴抛物线C1的顶点P(0,-4),抛物线C2的顶点Q(m,-4),
∴PQ=|m|,同(1)的方法得,M(
,
-4);
由“和谐线”的定义,易知,△PMQ是等腰直角三角形,
∴
-4+4=
|m|,
∴m=-2或m=2,
∴抛物线C2的解析式为y=(x-2)2-4或y=(x+2)2-4.
(3)当点N在x轴负半轴上时,如图,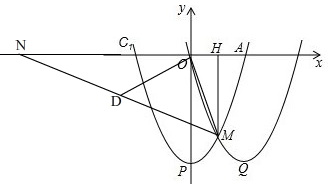
由(2)知,M(1,-3),抛物线C2过原点,
∴直线OM的解析式为y=-3x,
过点O作OD⊥OM,截取OD=OM,
∴△ODM是等腰直角三角形,
∴∠ODM=45°,
∵∠DON+∠MOA=90°,∠OMH+∠MOH=90°,
∴∠DON=∠OMH,
∵∠OMH=∠AMH,
∴∠AMH=∠DON,
∴直线OD的解析式为y=
x,
设点D的坐标为(3m,m)(m<0),
∴9m2+m2=10,
∴m=1(舍)或m=-1,
∴D(-3,-1),
∵M(1,-3),
∴直线DM的解析式为y=-
x-
,
令y=0,得-
x-
=0,
∴x=-5,
∴N(-5,0),
同理可得,x轴正半轴上的一个N点的坐标为(7,0).
即:满足条件的点N(-5,0)或(7,0).
∴抛物线C2的解析式为y=(x-m)2-4=x2-2mx+m2-4②,
联立①②得,x=
| m |
| 2 |
| m2 |
| 4 |
∴M(
| m |
| 2 |
| m2 |
| 4 |
(2)设抛物线C1:y=x2-4的和谐线抛物线C2的解析式为y=(x-m)2-4,
∴抛物线C1的顶点P(0,-4),抛物线C2的顶点Q(m,-4),
∴PQ=|m|,同(1)的方法得,M(
| m |
| 2 |
| m2 |
| 4 |
由“和谐线”的定义,易知,△PMQ是等腰直角三角形,
∴
| m2 |
| 4 |
| 1 |
| 2 |
∴m=-2或m=2,
∴抛物线C2的解析式为y=(x-2)2-4或y=(x+2)2-4.
(3)当点N在x轴负半轴上时,如图,

由(2)知,M(1,-3),抛物线C2过原点,
∴直线OM的解析式为y=-3x,
过点O作OD⊥OM,截取OD=OM,
∴△ODM是等腰直角三角形,
∴∠ODM=45°,
∵∠DON+∠MOA=90°,∠OMH+∠MOH=90°,
∴∠DON=∠OMH,
∵∠OMH=∠AMH,
∴∠AMH=∠DON,
∴直线OD的解析式为y=
| 1 |
| 3 |
设点D的坐标为(3m,m)(m<0),
∴9m2+m2=10,
∴m=1(舍)或m=-1,
∴D(-3,-1),
∵M(1,-3),
∴直线DM的解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
令y=0,得-
| 1 |
| 2 |
| 5 |
| 2 |
∴x=-5,
∴N(-5,0),
同理可得,x轴正半轴上的一个N点的坐标为(7,0).
即:满足条件的点N(-5,0)或(7,0).
看了 在平面直角坐标系xOy中,把...的网友还看了以下:
如图,直线AB是一次函数y=x+a的图象,直线AC是一次函数y=-2x+b的图象,(b》a》0), 2020-05-13 …
如图所示底座A上装有长0.5m的直立杆总质量为2KG杆上套有质量为0.5K歌的小环B如图所示的装置 2020-05-17 …
如图所示的装置中底座A上有长0.5m的直立杆,总质量为M=2kg,杆上套有质量为m=0.5kg的小 2020-05-17 …
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t的变化如图所示(0—2s力为 -1 2020-05-17 …
周叔叔买了图辆新汽车,p图表示0是v开车从成都到都江堰行驶路程与耗油量之间0关系.(1)行驶路程与 2020-06-21 …
如图所示,已知直线L经过A(4,0)和B(0,4)两点,它与抛物线y=a(x的平方)在第……(数学 2020-07-13 …
如图所示,直角坐标系xOy平面竖直,y轴竖直向上,平面内有沿竖直方向的匀强电场(图中未画出),由x 2020-07-17 …
一个物体沿直线运动,从t=0时刻开始,物体的xt-t的图象如图所示,图线与纵、横坐标轴的交点分别为 2020-07-21 …
在做《研究匀变速直线运动》的实验中,打点计时器采用的是(选“交流”或“直流”)电源;实验中得到一条纸 2020-11-17 …
加工一个零件,图纸上注明它的直径是Φ50,其中50表示直径是50mm,+0.02表示合格的直径最大只 2020-11-26 …