早教吧作业答案频道 -->数学-->
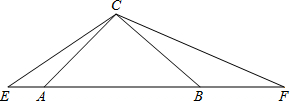
如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.
题目详情
如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.

▼优质解答
答案和解析
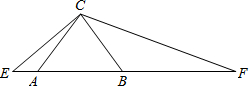 证明:∵△ABC为等腰直角三角形,∠ACB=90°,
证明:∵△ABC为等腰直角三角形,∠ACB=90°,
∴AC=BC,
∴∠CAB=∠CBA=45°,
∴∠CAE=180°-45°=135°,
同理∠CBF=135°,
∴∠CAE=∠CBF,
∵∠ECF=135°,∠ACB=90°,
∴∠ECA+∠BCF=45°,
∵∠ECA+∠E=∠CAB=45°,
∴∠E=∠BCF,
∵∠CAE=∠CBF,
∴△ECA∽△CFB;
∵AB=x,∠CAB=45°,∠ACB=90°,AC=BC,
∴sin45°=
,
∴CB=
x=AC,
∵由(1)知△ECA∽△CFB,
∴
=
,
∴
=
,
∴y=
x2,
即y与x之间的函数关系式是y=
x2.
 证明:∵△ABC为等腰直角三角形,∠ACB=90°,
证明:∵△ABC为等腰直角三角形,∠ACB=90°,∴AC=BC,
∴∠CAB=∠CBA=45°,
∴∠CAE=180°-45°=135°,
同理∠CBF=135°,
∴∠CAE=∠CBF,
∵∠ECF=135°,∠ACB=90°,
∴∠ECA+∠BCF=45°,
∵∠ECA+∠E=∠CAB=45°,
∴∠E=∠BCF,
∵∠CAE=∠CBF,
∴△ECA∽△CFB;
∵AB=x,∠CAB=45°,∠ACB=90°,AC=BC,
∴sin45°=
| CB |
| x |
∴CB=
| ||
| 2 |
∵由(1)知△ECA∽△CFB,
∴
| AE |
| CB |
| AC |
| BF |
∴
| 2 | ||||
|
| ||||
| y |
∴y=
| 1 |
| 4 |
即y与x之间的函数关系式是y=
| 1 |
| 4 |
看了 如图,在等腰三角形ABC中,...的网友还看了以下:
点A,B在数轴上分别表示有理数a,b(不妨设A点在B点左侧),A,B两点间的距离表示为|AB|,设 2020-05-16 …
对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设A={两次都击中飞机},B={两次都没击中飞机} 2020-06-16 …
如图,∠a、∠β是△ABC的外角,(1)如果∠a+∠β=260°,那么∠C=°(2)∠a+∠β能等 2020-07-30 …
求高手解一道关于导数的题啊!己知f(x)=x的三次方-x(1)求曲线y=f(x)在点M(t,f(t 2020-08-02 …
已知函数f(x)=x^3-x(1)求曲线y=f(x)在M(t,f(t))处(2)设a>0,如果过点P 2020-11-03 …
设A是如下形式的2行3列的数表,满足性质P:a,b,c,d,e,f∈[-1,1],且a+b+c+d+ 2020-11-17 …
设A是如下形式的2行3列的数表,abcdef满足性质P:a,b,c,d,e,f,且a+b+c+d+e 2020-11-17 …
设A是如下形式的2行3列的数表,abcdef满足性质P:a,b,c,d,e,f∈[-1,1],且a+ 2020-11-17 …
(2012•北京)设A是如下形式的2行3列的数表,abcdef满足性质P:a,b,c,d,e,f∈[ 2020-11-17 …
对飞机连续射击两次,每次发射一枚炮弹.设A={两次都击中飞机},B={两次都没击中飞机},C={恰有 2020-12-01 …