在等腰△ABC中，∠ABC=∠C=40°，延长AB至点D，使AD=BC，求∠BCD的度数．

Question

在等腰△ABC中，∠ABC=∠C=40°，延长AB至点D，使AD=BC，求∠BCD的度数．

Answer 1

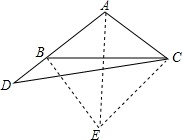如图所示，∵在等腰△ABC中，∠ABC=∠C=40°，
∴∠BAC=180°-40°-40°=100°．
以BC为一边在△ABC外作等边△BCE，连接AE，
∴BE=CE=BC，∠BEC=∠BCE=60°，
在△ABE与△ACE中，
∵

AB=AC

AE=AE

BE=CE

∴△ABE≌△ACE（SSS），
∴∠CEA=∠BEA=(1)/(2)×60°=30°，
∵∠BAC=100°，
∴∠ABC=∠ACB=40°，
∴∠ACE=∠CAD=100°，
在△ACE与△CAD中，
∵

AD=CE

∠ACE=∠CAD

AC=AC

∴△ACE≌△CAD（SAS），
∴∠D=∠CEA=30°，
在△ACD中，∠ACD=180°-∠D-∠A=50°，
∴∠BCD=∠ACD-∠ACB=10°．