早教吧作业答案频道 -->数学-->
如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.(1)求证:BCAB=EFDE;(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(
题目详情
如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.
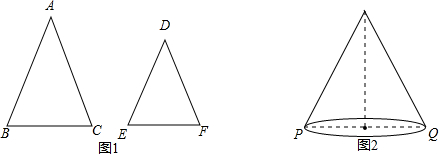
(1)求证:
=
;
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即T(A)=
=
,如T(60°)=1.
①理解巩固:T(90°)=___,T(120°)=___,若α是等腰三角形的顶角,则T(α)的取值范围是___;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
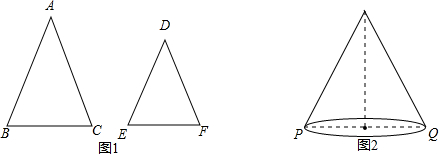
(1)求证:
| BC |
| AB |
| EF |
| DE |
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即T(A)=
| ∠A的对边(底边) |
| ∠A的邻边(腰) |
| BC |
| AB |
①理解巩固:T(90°)=___,T(120°)=___,若α是等腰三角形的顶角,则T(α)的取值范围是___;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
▼优质解答
答案和解析
(1)∵AB=AC,DE=DF,
∴
=
,
又∵∠A=∠D,
∴△ABC∽△DEF,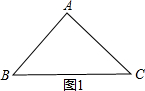
∴
=
;
(2)①如图1,∠A=90°,AB=AC,
则
=
,
∴T(90°)=
,
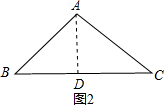 如图2,∠A=90°,AB=AC,
如图2,∠A=90°,AB=AC,
作AD⊥BC于D,
则∠B=60°,
∴BD=
AB,
∴BC=
AB,
∴T(120°)=
;
∵AB-AC<BC<AB+AC,
∴0<T(α)<2,
故答案为:
;
;0<T(α)<2;
②∵圆锥的底面直径PQ=8,
∴圆锥的底面周长为8π,即侧面展开图扇形的弧长为8π,
设扇形的圆心角为n°,
则
=8π,
解得,n=160,
∵T(80°)≈1.29,
∴蚂蚁爬行的最短路径长为1.29×9≈11.6.
∴
| AB |
| DE |
| AC |
| DF |
又∵∠A=∠D,
∴△ABC∽△DEF,

∴
| BC |
| AB |
| EF |
| DE |
(2)①如图1,∠A=90°,AB=AC,
则
| BC |
| AB |
| 2 |
∴T(90°)=
| 2 |
 如图2,∠A=90°,AB=AC,
如图2,∠A=90°,AB=AC,作AD⊥BC于D,
则∠B=60°,
∴BD=
| ||
| 2 |
∴BC=
| 3 |
∴T(120°)=
| 3 |
∵AB-AC<BC<AB+AC,
∴0<T(α)<2,
故答案为:
| 2 |
| 3 |
②∵圆锥的底面直径PQ=8,
∴圆锥的底面周长为8π,即侧面展开图扇形的弧长为8π,
设扇形的圆心角为n°,
则
| n×π×9 |
| 180 |
解得,n=160,
∵T(80°)≈1.29,
∴蚂蚁爬行的最短路径长为1.29×9≈11.6.
看了 如图1,△ABC和△DEF中...的网友还看了以下:
已知集合A中含有三个元素,a-2,12,2a的平方+5a,又-3属于A,求的a值 2020-04-05 …
选取四个正整数a,b,c,d,且a<b<c<d,使得1a+1b+1c+1d是一个整数,那么符合要求 2020-05-14 …
(1)一个正数的平方根是a+3与2a﹣15,求a的值.(2)已知,求的立方根.(3)已知x、y为实 2020-05-14 …
例1:若60a=3,60b=5.求121−a−b2(1−b)的值. 2020-06-03 …
已知a^2+b^2+c^2-ab-3b-2c+4=0,求的a+b+c值这道题我上网查过答案,我要推 2020-06-11 …
如图示匀强电场宽度为L,一带电粒子质量为m,带电荷量为+q,从图中A点以V0垂直于场强方向进入匀强 2020-06-12 …
设总体X~U(1,θ),参数θ>1未知,X1,…,Xn是来自X的简单随机样本.①求θ的矩估计和极大 2020-06-12 …
已知某正数的两个平方根分别是a+3和2a-15,b的立方根是-2.求-b-a的算术平方根. 2020-06-13 …
设全集为U,集合A,B是U的子集,定义集合A,B的运算:A*B={x|x∈A或x∈B且x∉A∩B} 2020-06-16 …
已知a、b为已知数,关于x的方程a(a-4)kx-b(b+6)=9-4kx,无论k为何值时,它的根 2020-07-09 …