早教吧作业答案频道 -->数学-->
如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°求证:DE2=AD2+BE2.
题目详情
如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°
求证:DE2=AD2+BE2.
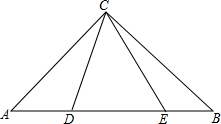
求证:DE2=AD2+BE2.

▼优质解答
答案和解析
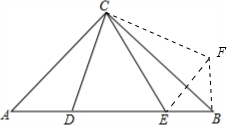 证明:如图,将△ADC绕点C逆时针旋转90°到△CBF的位置;
证明:如图,将△ADC绕点C逆时针旋转90°到△CBF的位置;
则CD=CE,AD=BF;∠BCF=∠ACD,∠CBF=∠A;
∵BC=AC,∠ACB=90°,
∴∠A=∠ABC=∠CBF=45°,
∴∠EBF=90°,EF2=BE2+BF2=AD2+BE2;
∵∠DCE=45°,∠ACB=90°,
∴∠ACD+∠BCE=90°-45°=45°,而∠ACD=∠BCF,
∴∠ECF=∠ECD=45°;在△DCE与△FCE中,
,
∴△DCE≌△FCE(SAS),
∴DE=EF,
∴DE2=AD2+BE2.
 证明:如图,将△ADC绕点C逆时针旋转90°到△CBF的位置;
证明:如图,将△ADC绕点C逆时针旋转90°到△CBF的位置;则CD=CE,AD=BF;∠BCF=∠ACD,∠CBF=∠A;
∵BC=AC,∠ACB=90°,
∴∠A=∠ABC=∠CBF=45°,
∴∠EBF=90°,EF2=BE2+BF2=AD2+BE2;
∵∠DCE=45°,∠ACB=90°,
∴∠ACD+∠BCE=90°-45°=45°,而∠ACD=∠BCF,
∴∠ECF=∠ECD=45°;在△DCE与△FCE中,
|
∴△DCE≌△FCE(SAS),
∴DE=EF,
∴DE2=AD2+BE2.
看了 如图所示,在等腰△ABC中,...的网友还看了以下:
在矩形ABCD中,对角线AC=10(AB>BC),点B到AC的距离为4,E、F是对角线AC上两个动点 2020-03-30 …
如图,△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD的平分线上一点,EB=EC,过点 2020-07-09 …
在Rt△ABC中,∠ACB=90°,M为AB上一点,MD⊥AC于点D,MC与BD交于点E,过点E作 2020-07-17 …
如图,在直角三角形ABC中,点E在线段AB上,过点E作EH⊥AC交AC于点H,点F在BC的延长线上 2020-07-19 …
如图,在△ABC中,∠ACB=90°,∠A=60°,AC=3,点D是边AB上的动点(点D与点A、B 2020-07-20 …
如图,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=C 2020-07-31 …
如图,在三角形ABC中,AB=AC,D是边BC延长线上一点,E是边AC上一点,如果角EBC=角D, 2020-08-01 …
已知边长为1的正方形ABCD中,P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB 2020-08-03 …
已知△ABC的面积为1,D,E分别是AB,AC边上的点,CD,BE交于F点,过点F作FM‖AB,FN 2020-11-03 …
如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,BF=DE 2020-11-03 …