早教吧作业答案频道 -->数学-->
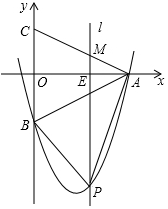
如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=0.5x2-3.5x-4经过A、B两点.若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分
题目详情
如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=0.5x2-3.5x-4经过A、B两点.若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连结PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积.

▼优质解答
答案和解析
对于抛物线y=0.5x2-3.5x-4中,令y=0,得到0.5x2-3.5x-4=0解得x=-1或8,
∴A(8,0),B(0,-4),
∵AB=AC,OA⊥BC,
∴OB=OC,
∴C(0,4),
设直线AC的解析式为y=kx+b,由A(8,0),C(0,4)得到
,
解得
,
∴直线AC的解析式为y=-
x+4,
∵直线l以每秒2个单位长度的速度向右平移,时间为t,
∴OE=2t,设P(2t,2t2-7t-4),则M(2t,4-t),
∵BC=8,PM=4-t-(2t2-7t-4)=-2t2+6t+8,AE=8-2t,
S=S梯形BCMP+S△PMA=
•(-2t2+6t+8+8)×2t+
(8-2t)(-2t2+6t+8)=-8t2+32t+32=-8(t-2)2+64,
∵-8<0,
∴t=2时,四边形PBCA的最大面积为64.
∴A(8,0),B(0,-4),
∵AB=AC,OA⊥BC,
∴OB=OC,
∴C(0,4),
设直线AC的解析式为y=kx+b,由A(8,0),C(0,4)得到
|
解得
|
∴直线AC的解析式为y=-
| 1 |
| 2 |
∵直线l以每秒2个单位长度的速度向右平移,时间为t,
∴OE=2t,设P(2t,2t2-7t-4),则M(2t,4-t),
∵BC=8,PM=4-t-(2t2-7t-4)=-2t2+6t+8,AE=8-2t,
S=S梯形BCMP+S△PMA=
| 1 |
| 2 |
| 1 |
| 2 |
∵-8<0,
∴t=2时,四边形PBCA的最大面积为64.
看了 如图,在等腰三角形ABC中,...的网友还看了以下:
设a,b是异面直线,直线a在平面α内,直线b在平面β内,且a平行β,b平行α,求证:α平行β 2020-04-05 …
高中几何证明题~有关平行~设a,b是异面直线,直线a在平面A内,直线b在平面B内,且a平行于B,直 2020-06-03 …
(2014•黔西南州)如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=35°,则∠2 2020-06-23 …
怎么选择断链桩号拜托了各位谢谢例:某路线A在定测时,在AK2+356.400处开始局部改线,老路线 2020-06-26 …
三个导体元件A、B、C的伏安特性曲线分别如图线a、b、c所示.当它们串联后接在6V稳压直流电源两端 2020-07-15 …
有下列四个命题:①若直线a垂直于直线b在平面α内的射影,则a⊥b;②若OM∥O1M1且ON∥O1N 2020-07-16 …
有a、b、c、d四条直线,从直线a开始,按直线方向从1开始依次在a、b、c、d上面写了自然数1、2 2020-07-21 …
如图,点O在直线AB上,点M,N在直线AB外,若MO⊥AB,NO⊥AB,垂足均为O,则可得点N在直 2020-07-29 …
下列命题中,正确的是()A.直线a平行于平面α内的一条直线b,则a∥αB.直线a垂直于平面α的斜线 2020-07-30 …
设平面α与平面β相交于直线m,直线a在平面α内.直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b 2020-07-31 …