．如图，△ABC是等边三角形，D为BC边上一个动点（D与B、C均不重合），AD=AE，∠DAE=60°，连接CE．（1）求证：△ABD≌△ACE；（2）求证：CE平分∠ACF；（3）若AB=2，当四边形ADCE的周长取

Question

．如图，△ABC是等边三角形，D为BC边上一个动点（D与B、C均不重合），AD=AE，∠DAE=60°，连接CE．

（1）求证：△ABD≌△ACE；

（2）求证：CE平分∠ACF；

（3）若AB=2，当四边形ADCE的周长取最小值时，求BD的长．

Answer 1

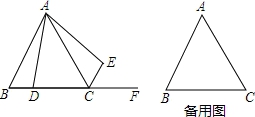
【考点】全等三角形的判定与性质；等边三角形的性质．

【分析】（1）由于AB=AC，AD=AE，所以只需证∠BAD=∠CAE即可得结论；

（2）证明∠ACE和∠ECF都等于60°即可；

（3）将四边形ADCE的周长用AD表示，AD最小时就是四边形ADCE的周长最小，根据垂线段最短原理，当AD⊥BC时，AD最小，此时BD就是BC的一半．

【解答】（1）证明：∵△ABC是等边三角形，

∴AB=AC，∠BAC=60°，

∵∠DAE=60°，

∴∠BAD+∠DAC=∠CAE+∠DAC，

即∠BAD=∠CAE，

在△ABD和△ACE中，

，

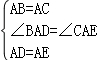∴△ABD≌△ACE．

（2）证明：∵△ABC是等边三角形，

∴∠B=∠BCA=60°，

∵△ABD≌△ACE，

∴∠ACE=∠B=60°，

∵△ABD≌△ACE，

∴∠ACE=∠B=60°，

∴∠ECF=180﹣∠ACE﹣∠BCA=60°，

∴∠ACE=∠ECF，

∴CE平分∠ACF．

（3）∵△ABD≌△ACE，

∴CE=BD，

∵△ABC是等边三角形，

∴AB=BC=AC=2，

∴四边形ADCE的周长=CE+DC+AD+AE=BD+DC+2AD=2+AD，

根据垂线段最短，当AD⊥BC时，AD值最小，四边形ADCE的周长取最小值，

∵AB=AC，

∴BD===1．

【点评】此题主要考查了全等三角形的判定和性质定理以及垂线段最短原理，关键是找出能使三角形全等的条件，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，全等三角形的对应边相等，对应角相等．