早教吧作业答案频道 -->数学-->
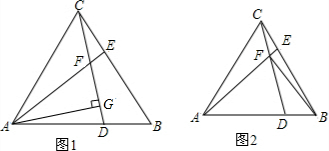
如图1,已知△ABC是等边三角形,D、E分别是AB、BC上的点,且BD=CE,AE、CD交于点F.(1)求证:△ACE≌△CBD;(2)过A作AG⊥CD于G,求证:AF=2FG;(3)如图2,若BF⊥AF,求CFAF的值.
题目详情
如图1,已知△ABC是等边三角形,D、E分别是AB、BC上的点,且BD=CE,AE、CD交于点F.
(1)求证:△ACE≌△CBD;
(2)过A作AG⊥CD于G,求证:AF=2FG;
(3)如图2,若BF⊥AF,求
的值.
(1)求证:△ACE≌△CBD;
(2)过A作AG⊥CD于G,求证:AF=2FG;
(3)如图2,若BF⊥AF,求
| CF |
| AF |

▼优质解答
答案和解析
(1)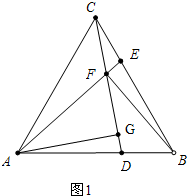 证明:如图1,∵△ABC是等边三角形,
证明:如图1,∵△ABC是等边三角形,
∴AC=BC,∠ACE=∠B=60°,
在△ACE和△CBD中,
,
∴△ACE≌△CBD
(2)∵△ACE≌△CBD,
∴∠CAE=∠BCD,
∵∠AFG=∠CAE+∠ACF=∠BCD+∠ACF=∠ACB=60°,
∵AG⊥CD,
∴∠AGF=90°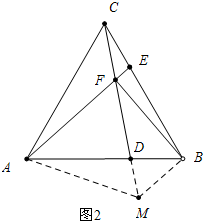
∴∠FAG=30°,
∴AF=2FG.
(3)如图2中,延长FD到M,使得∠FAM=60°,连接BM.
∵∠AFM=∠FAM=∠AMF=60°,
∴△AFM是等边三角形,
∴AF=FM=AM,
∵∠CAB=∠FAM=60°,
∴∠CAF=∠MAB,
在△CAF和△BAM中,
,
∴△CAF≌△BAM,
∴CF=BM,
∵AF⊥BF,∠AFD=60°,
∴∠MFB=30°,
∵∠AMD=∠ABC=60°,
∴AMBC四点共圆,
∴∠AMB+∠ACB=180°,
∴∠FMB=60°,
∴∠FBM=180°-∠MFB-∠FMB=90°,
∴FM=2BM,
∴AF=2CF
∴
=
.
 证明:如图1,∵△ABC是等边三角形,
证明:如图1,∵△ABC是等边三角形,∴AC=BC,∠ACE=∠B=60°,
在△ACE和△CBD中,
|
∴△ACE≌△CBD
(2)∵△ACE≌△CBD,
∴∠CAE=∠BCD,
∵∠AFG=∠CAE+∠ACF=∠BCD+∠ACF=∠ACB=60°,
∵AG⊥CD,
∴∠AGF=90°

∴∠FAG=30°,
∴AF=2FG.
(3)如图2中,延长FD到M,使得∠FAM=60°,连接BM.
∵∠AFM=∠FAM=∠AMF=60°,
∴△AFM是等边三角形,
∴AF=FM=AM,
∵∠CAB=∠FAM=60°,
∴∠CAF=∠MAB,
在△CAF和△BAM中,
|
∴△CAF≌△BAM,
∴CF=BM,
∵AF⊥BF,∠AFD=60°,
∴∠MFB=30°,
∵∠AMD=∠ABC=60°,
∴AMBC四点共圆,
∴∠AMB+∠ACB=180°,
∴∠FMB=60°,
∴∠FBM=180°-∠MFB-∠FMB=90°,
∴FM=2BM,
∴AF=2CF
∴
| CF |
| AF |
| 1 |
| 2 |
看了 如图1,已知△ABC是等边三...的网友还看了以下:
已知f(x)是定义在[-1,1]上的函数,f(x)=-f(-x),且f(1)=1,若a,b∈[-1 2020-07-16 …
1.已知函数f(x)=x^3+x(x∈R)若a,b,c∈R,且a+b>0,b+c>0,a+c>0, 2020-07-30 …
在锐角三角形ABC中,AB≠AC,AD是高,H是AD上一点,连BH并延长交AC于E,连接CH并延长 2020-07-30 …
已知函数f(x)是R上的增函数,对实数a,b,若a+b>0,则有()A.f(a)+f(b)>f(- 2020-08-01 …
1.若集合X={x/x=2n+1,n∈Z},Y={y/y=4k±1,k∈z},试证明X=Y.2.已知 2020-10-31 …
已经知道,设f是[a.b]上的可积函数,若f(x)>=0,x∈[a,b],则定积分∫a^bf(x)d 2020-11-01 …
(1/2)设抛物线C:x^2=2py的焦点为F,准线为l,A为C上一点,已知F为圆心,FA为半径的圆 2020-11-27 …
已知函数f(x)=a*b^x+c,x∈[0,正无穷)的值域为[-2,3),那么函数f(x)的一个解析 2020-12-08 …
已知函数f(x)=ax+b/x+c(a>0)的图像在点,(1,f(1))处的切线方程为y=x-1.( 2020-12-08 …
已知f(x)=x(x-a)(x-b),点A(s,f(s)),B(t,f(t)).(Ⅰ)若a=b=1, 2020-12-22 …