早教吧作业答案频道 -->数学-->
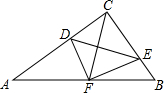
如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为.
题目详情
如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为___.

▼优质解答
答案和解析
 由折叠可得,∠DCE=∠DFE=90°,
由折叠可得,∠DCE=∠DFE=90°,
∴D,C,E,F四点共圆,
∴∠CDE=∠CFE=∠B,
又∵CE=FE,
∴∠CFE=∠FCE,
∴∠B=∠FCE,
∴CF=BF,
同理可得,CF=AF,
∴AF=BF,即F是AB的中点,
∴Rt△ABC中,CF=
AB=5,
由D,C,E,F四点共圆,可得∠DFC=∠DEC,
由∠CDE=∠B,可得∠DEC=∠A,
∴∠DFC=∠A,
又∵∠DCF=∠FCA,
∴△CDF∽△CFA,
∴CF2=CD×CA,即52=CD×8,
∴CD=
,
故答案为:
.
 由折叠可得,∠DCE=∠DFE=90°,
由折叠可得,∠DCE=∠DFE=90°,∴D,C,E,F四点共圆,
∴∠CDE=∠CFE=∠B,
又∵CE=FE,
∴∠CFE=∠FCE,
∴∠B=∠FCE,
∴CF=BF,
同理可得,CF=AF,
∴AF=BF,即F是AB的中点,
∴Rt△ABC中,CF=
| 1 |
| 2 |
由D,C,E,F四点共圆,可得∠DFC=∠DEC,
由∠CDE=∠B,可得∠DEC=∠A,
∴∠DFC=∠A,
又∵∠DCF=∠FCA,
∴△CDF∽△CFA,
∴CF2=CD×CA,即52=CD×8,
∴CD=
| 25 |
| 8 |
故答案为:
| 25 |
| 8 |
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
1.在一幅地图上,比例尺为1:300000,量得A、B两地的距离为18厘米,则A、B两地的实地距离 2020-04-07 …
证明空间中的四点A,B,C,D共面的充分必要条件是它们所对应的位置向量a,b,c,d满足(d,b, 2020-05-13 …
平行四边形ABCD中ac^2+bd^2=2ab^2类比到平行六面体ABCD-A'B'C'D'是什么 2020-05-13 …
一道MATLAB题~写出执行以下代码后C,D,E的值A=[1,2,3;4:6;7:9];C=[A; 2020-06-12 …
关于java的swap比如有[a,b,c,d,e]5个字母...用swap交换为[d,e,c,a, 2020-07-17 …
已知a.b.c.d都是正整数,并且a^5=b^4,c^3=d^2,c-a=9,则a-b的值是多少 2020-07-21 …
数学中有关集合表达式的写法,添加元素问题.具体见补充例如有一个集合A={a,b,c},另有一个元素 2020-07-23 …
若非空集合A={x|2a+1£x£3a-5}B={x|3£x£22}则能使AÍB源网成立的所有a的 2020-07-27 …
a、b、c都是大于0的数,而且a×0.9=b÷0.9=C.a、b、c比较,按从大到小排列应是任意一 2020-07-30 …
图为以极地为中心的昼夜状况示意图(阴影部分表示黑夜)读图回答题。1.A点的地方时是2.该日的日期最接 2020-11-21 …