早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=12∠A.(1)求证:BC是O的切线;(2)若sinB=35,O的半径为r,求△EHG的面
题目详情
如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的 O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=
∠A.
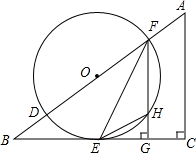
(1)求证:BC是 O的切线;
(2)若sinB=
, O的半径为r,求△EHG的面积(用含r的代数式表示).
| 1 |
| 2 |

(1)求证:BC是 O的切线;
(2)若sinB=
| 3 |
| 5 |
▼优质解答
答案和解析
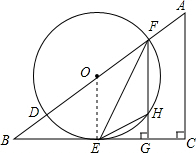 (1)证明:连接OE,
(1)证明:连接OE,
∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,
∴FG∥AC,
∴∠OFG=∠A,
∴∠OFE=
∠OFG,
∴∠OFE=∠EFG,
∵OE=OF,
∴∠OFE=∠OEF,
∴∠OEF=∠EFG,
∴OE∥FG,
∴OE⊥BC,
∴BC是 O的切线;
(2) ∵在Rt△OBE中,sinB=
, O的半径为r,
∴OB=
r,BE=
r,
∴BF=OB+OF=
r,
∴FG=BF•sinB=
r,
∴BG=
=
r,
∴EG=BG-BE=
r,
∴S△FGE=
EG•FG=
r2,EG:FG=1:2,
∵BC是切线,
∴∠GEH=∠EFG,
∵∠EGH=∠FGE,
∴△EGH∽△FGE,
∴
=(
)=
,
∴S△EHG=
S△FGE=
r2.
 (1)证明:连接OE,
(1)证明:连接OE,∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,
∴FG∥AC,
∴∠OFG=∠A,
∴∠OFE=
| 1 |
| 2 |
∴∠OFE=∠EFG,
∵OE=OF,
∴∠OFE=∠OEF,
∴∠OEF=∠EFG,
∴OE∥FG,
∴OE⊥BC,
∴BC是 O的切线;
(2) ∵在Rt△OBE中,sinB=
| 3 |
| 5 |
∴OB=
| 5 |
| 3 |
| 4 |
| 3 |
∴BF=OB+OF=
| 8 |
| 3 |
∴FG=BF•sinB=
| 8 |
| 5 |
∴BG=
| BF2-FG2 |
| 32 |
| 15 |
∴EG=BG-BE=
| 4 |
| 5 |
∴S△FGE=
| 1 |
| 2 |
| 16 |
| 25 |
∵BC是切线,
∴∠GEH=∠EFG,
∵∠EGH=∠FGE,
∴△EGH∽△FGE,
∴
| S△EGH |
| S△FGE |
| EG |
| FG |
| 1 |
| 4 |
∴S△EHG=
| 1 |
| 4 |
| 4 |
| 25 |
看了 如图,在△ABC中,∠C=9...的网友还看了以下:
定义在R上的奇函数f(x)是增函数,偶函数g(x)在区间零到正无穷左闭右开上的图像与f(x)的图像重 2020-03-31 …
线性代数问题.2阶矩阵A1012,验证对任意的f(x) g(x),是否都有f(A) g(A)=g( 2020-05-13 …
设f(x)、g(x)是在闭区间a,b上的两个连续函数,而f(a)>g(a),f(b) 2020-06-18 …
设f(x),g(x)在[a,b]上连续,且均为严格单增的正函数,证明:存在c€(a,b)使f(b) 2020-06-18 …
如何证矩阵函数的交换性:f(A)g(A)=g(A)f(A)请不吝赐教! 2020-06-24 …
f(x)g'(x)>f'(x)g(x)af(b)g(x)D.f(x)g(a)>f(a)g(x)要有 2020-07-07 …
某超市员工将各品牌洗发液摆上货架,已知洗发液有E、F、G、H、I等五个品牌,在货架上从左向右排列, 2020-07-12 …
设f(x),g(x)在[a,b]上连续,在(a,b)内可导,且g(x)不等于0,f(a)g(b)= 2020-07-21 …
这个Mathematica三维图为什么画不出来w=1403L=150a=650w1=w/2//Nr= 2020-10-31 …
设函数fx,gx在(a,b)上连续且可导,在(a,.b〉内二介可导,且存在相等的最大值,f(a)=g 2020-11-03 …