早教吧作业答案频道 -->数学-->
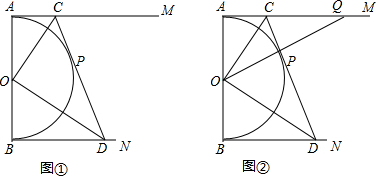
如图①,半圆O的直径AB=6,AM和BN是它的两条切线,CP与半圆O相切于点P,并于AM,BN分别相交于C,D两点.(1)请直接写出∠COD的度数;(2)求AC•BD的值;(3)如图②,连接OP并延长交AM于点Q
题目详情
如图①,半圆O的直径AB=6,AM和BN是它的两条切线,CP与半圆O相切于点P,并于AM,BN分别相交于C,D两点.
(1)请直接写出∠COD的度数;
(2)求AC•BD的值;
(3)如图②,连接OP并延长交AM于点Q,连接DQ,试判断△PQD能否与△ACO相似?若能相似,请求AC:BD的值;若不能相似,请说明理由.
(1)请直接写出∠COD的度数;
(2)求AC•BD的值;
(3)如图②,连接OP并延长交AM于点Q,连接DQ,试判断△PQD能否与△ACO相似?若能相似,请求AC:BD的值;若不能相似,请说明理由.

▼优质解答
答案和解析
(1)∠COD=90°.
理由:如图①中,∵AB是直径,AM、BN是切线,
∴AM⊥AB,BN⊥AB,
∴AM∥BN,
∵CA、CP是切线,
∴∠ACO=∠OCP,同理∠ODP=∠ODB,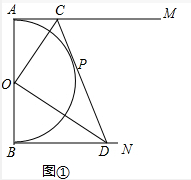
∵∠ACD+∠BDC=180°,
∴2∠OCD+2∠ODC=180°,
∴∠OCD+∠ODC=90°,
∴∠COD=90°.
(2)如图①中,∵AB是直径,AM、BN是切线,
∴∠A=∠B=90°,
∴∠ACO+∠AOC=90°,
∵∠COD=90°,
∴∠BOD+∠AOC=90°,
∴∠ACO=∠BOD,
∴RT△AOC∽RT△BDO,
∴
=
,
即AC•BD=AO•BO,
∵AB=6,
∴AO=BO=3,
∴AC•BD=9.
(3)△PQD能与△ACQ相似.
∵CA、CP是 O切线,
∴AC=CP,∠1=∠2,
∵DB、DP是 O切线,
∴DB=DP,∠B=∠OPD=90°,OD=OD,
∴RT△ODB≌RT△ODP,
∴∠3=∠4,
①如图②中,当△PQD∽△ACO时,∠5=∠1,
∵∠ACO=∠BOD,即∠1=∠3,
∴∠5=∠4,
∴DQ=DO,
∴∠PDO=∠PDQ,
∴△DCQ≌△DCO,
∴∠DCQ=∠2,
∵∠1+∠2+∠DCQ=180°,
∴∠1=60°=∠3,
在RT△ACO,RT△BDO中,分别求得AC=
,BD=3
,
∴AC:BD=1:3.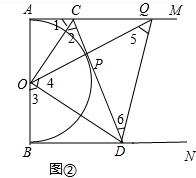
②如图②中,当△PQD∽△AOC时,∠6=∠1,
∵∠2=∠1,
∴∠6=∠2,
∴CO∥QD,
∴∠1=∠CQD,
∴∠6=∠CQD,
∴CQ=CD,
∵S△CDQ=
•CD•PQ=
•CQ•AB,
∴PQ=AB=6,
∵CO∥QD,
∴
=
,即
=
,
∴AC:BD=1:2
理由:如图①中,∵AB是直径,AM、BN是切线,
∴AM⊥AB,BN⊥AB,
∴AM∥BN,
∵CA、CP是切线,
∴∠ACO=∠OCP,同理∠ODP=∠ODB,

∵∠ACD+∠BDC=180°,
∴2∠OCD+2∠ODC=180°,
∴∠OCD+∠ODC=90°,
∴∠COD=90°.
(2)如图①中,∵AB是直径,AM、BN是切线,
∴∠A=∠B=90°,
∴∠ACO+∠AOC=90°,
∵∠COD=90°,
∴∠BOD+∠AOC=90°,
∴∠ACO=∠BOD,
∴RT△AOC∽RT△BDO,
∴
| AC |
| BO |
| AO |
| BD |
即AC•BD=AO•BO,
∵AB=6,
∴AO=BO=3,
∴AC•BD=9.
(3)△PQD能与△ACQ相似.
∵CA、CP是 O切线,
∴AC=CP,∠1=∠2,
∵DB、DP是 O切线,
∴DB=DP,∠B=∠OPD=90°,OD=OD,
∴RT△ODB≌RT△ODP,
∴∠3=∠4,
①如图②中,当△PQD∽△ACO时,∠5=∠1,
∵∠ACO=∠BOD,即∠1=∠3,
∴∠5=∠4,
∴DQ=DO,
∴∠PDO=∠PDQ,
∴△DCQ≌△DCO,
∴∠DCQ=∠2,
∵∠1+∠2+∠DCQ=180°,
∴∠1=60°=∠3,
在RT△ACO,RT△BDO中,分别求得AC=
| 3 |
| 3 |
∴AC:BD=1:3.

②如图②中,当△PQD∽△AOC时,∠6=∠1,
∵∠2=∠1,
∴∠6=∠2,
∴CO∥QD,
∴∠1=∠CQD,
∴∠6=∠CQD,
∴CQ=CD,
∵S△CDQ=
| 1 |
| 2 |
| 1 |
| 2 |
∴PQ=AB=6,
∵CO∥QD,
∴
| PC |
| PD |
| PO |
| PQ |
| AC |
| BD |
| 3 |
| 6 |
∴AC:BD=1:2
看了 如图①,半圆O的直径AB=6...的网友还看了以下:
数学概率.需求完整的解答.一位同学分别参加了三所大学自主招生笔试(各校试题不相同),如果该同学通过 2020-05-13 …
急:物体作匀变速直线运动,通过连续两段相同位移的平均速度分别为3米每秒物体作匀变速直线运动,通过连 2020-05-16 …
三个分数的和是2又十分之一,它们的分母相同,分子的比是1:2:3,这三个分数分别是()(三个分数的 2020-05-19 …
分数除法和比的应用的题一.1个分数分别与3分之2,7分之4相乘,相乘的两个积之和为7分之2这个分数 2020-05-20 …
三相表:三相四线3×220/380与3×380有什么区别?三相表:三相四线3×220/380与3× 2020-07-09 …
半径分别为1、3的两圆外切,半径分别为3、4、5的圆与这两个圆相切,这样的圆分别有几个? 2020-07-14 …
客、货两车分别分别从相距262.5千米的两地同时开出,相向而行,3.5小时相遇,已知客、货两车的速 2020-07-19 …
函数y=2sin(-2x+π/3)的相位和初相分别是什么?变形得y=2sin(2x+2π/3)所以 2020-07-30 …
甲、乙两个纸袋内各装有大小、形状相同的3卡片,甲袋的3张分别标有数字1、3、5,乙袋的3张分别标有 2020-08-01 …
其中“原”命题与“逆”命题都是真命题的有:1若a>0,b>0则a+b>02平行四边形的对角线互相平 2020-08-01 …