早教吧作业答案频道 -->数学-->
理解证明:如图1,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明△ABD≌△CAF;类比探究:如图2,点B,C在∠MAN的边AM、AN上,点E,F
题目详情
理解证明:如图1,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明△ABD≌△CAF;
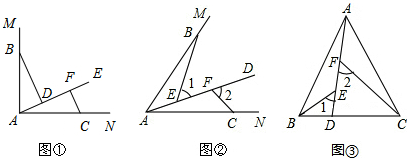
类比探究:如图2,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为___.

类比探究:如图2,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为___.
▼优质解答
答案和解析
理解证明:
证明:∵CF⊥AE,BD⊥AE,
∴∠ADB=∠CFA=90°,
∵∠MAN=90°,
∴∠ABD+∠BAD=90°,又∠CAF+∠BAD=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
,
∴△ABD≌△CAF;
类比探究:
证明:∵∠1=∠2,
∴∠ABE=∠CAF,
∵∠1=∠ABE+∠EAB,∠1=∠BAC,
∴∠ABE=∠CAF,
在△ABE和△CAF中,
,
∴△ABE≌△CAF;
拓展应用:∵△ABC的面积为15,CD=2BD,
∴△ABD的面积为15×
=5,
由类比探究得,△ABE≌△CAF,
∴△ACF与△BDE的面积之和=△ABD的面积=5,
故答案为:5.
证明:∵CF⊥AE,BD⊥AE,
∴∠ADB=∠CFA=90°,
∵∠MAN=90°,
∴∠ABD+∠BAD=90°,又∠CAF+∠BAD=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
|
∴△ABD≌△CAF;
类比探究:
证明:∵∠1=∠2,
∴∠ABE=∠CAF,
∵∠1=∠ABE+∠EAB,∠1=∠BAC,
∴∠ABE=∠CAF,
在△ABE和△CAF中,
|
∴△ABE≌△CAF;
拓展应用:∵△ABC的面积为15,CD=2BD,
∴△ABD的面积为15×
| 1 |
| 3 |
由类比探究得,△ABE≌△CAF,
∴△ACF与△BDE的面积之和=△ABD的面积=5,
故答案为:5.
看了 理解证明:如图1,∠MAN=...的网友还看了以下:
分解因式a(a-b-c)+b(c-a+b)+c(b-a+c)的结果是()A.(b+c-a)2B.( 2020-04-08 …
24 (a+b)/(c+d)=(√a^2+b^2)/√ (c^2+d^2)成立证明:(1)a/b= 2020-05-14 …
已知△ABC,内角A,B,C所对的边分别为a,b,c,且满足下列三个条件1.a^2+b^2=c^2 2020-05-23 …
有理数a、b在数轴上的对应点位置如图所示(1)用“<”连接0、-a、-b、-1(2)化简:|a|- 2020-07-20 …
35.a+b+c=26;(A)证明:(1)a、b、c成等比数列,且a,b+4,c成等差数列=/=> 2020-07-30 …
(急)一道基本不等式证明题(高一数学)证明bc/a+ac/b+ab/c≥a+b+c证明:(请看我的 2020-08-03 …
已知a、b、c满足a<b<c,ab+bc+ac=0,abc=1,则()A.|a+b|>|c|B.|a 2020-11-01 …
已知集合A={直线},B={平面},C=A∪B,若a∈A,b∈B,c∈C,则下列命题中正确的是()A 2020-11-02 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
7,如果事件ABC相互独立,则下列等式中正确的是()A,P(A+B+C)=P(A)+P(B)+P(C 2020-12-01 …