早教吧作业答案频道 -->数学-->
如图,已知抛物线y=-x2+bx+3与x轴相交于点A和点B(点A在点B的左侧),与y轴交于点C,且OB=OC,点D是抛物线的顶点,直线AC和BD交于点E.(1)求点D的坐标;(2)联结CD、BC,求∠DBC余切值;(3
题目详情
如图,已知抛物线y=-x2+bx+3与x轴相交于点A和点B(点A在点B的左侧),与y轴交于点C,且OB=OC,点D是抛物线的顶点,直线AC和BD交于点E.
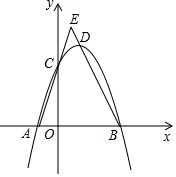
(1)求点D的坐标;
(2)联结CD、BC,求∠DBC余切值;
(3)设点M在线段CA延长线,如果△EBM和△ABC相似,求点M的坐标.

(1)求点D的坐标;
(2)联结CD、BC,求∠DBC余切值;
(3)设点M在线段CA延长线,如果△EBM和△ABC相似,求点M的坐标.
▼优质解答
答案和解析
(1)∵已知抛物线y=-x2+bx+3与y轴交于点C,
∴点C的坐标为:(0,3),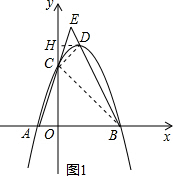
∵OB=OC,
∴点B的坐标为:(3,0),
∴-9+3b+3=0,
解得,b=2,
∴抛物线的解析式为:y=-x2+2x+3,
y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4);
(2)如图1,作DH⊥y轴于H,
则CH=DH=1,
∴∠HCD=∠HDC=45°,
∵OB=OC,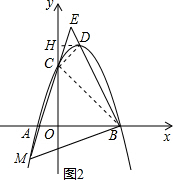
∴∠OCB=∠OBC=45°,
∴∠DCB=90°,
∴cot∠DBC=
=
=3;
(3)-x2+2x+3=0,
解得,x1=-1,x2=3,
∴点A的坐标为:(-1,0),
∴
=
,又
=
,
∴
=
,
∴Rt△AOC∽Rt△DCB,
∴∠ACO=∠DBC,
∵∠ACB=∠ACO+45°=∠DBC+∠E,
∴∠E=45°,
∵△EBM和△ABC相似,∠E=∠ABC=45°,
∴∠ACB=∠BME,
∴BM=BC,
设直线CA的解析式为:y=kx+b,
则
,
解得,
,
则直线CA的解析式为:y=3x+3,
设点M的坐标为(x,3x+3),
则(x-3)2+(3x+3)2=18,
解得,x1=0(舍去),x2=-
,
x2=-
时,y=-
,
∴点M的坐标为(-
,-
∴点C的坐标为:(0,3),

∵OB=OC,
∴点B的坐标为:(3,0),
∴-9+3b+3=0,
解得,b=2,
∴抛物线的解析式为:y=-x2+2x+3,
y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4);
(2)如图1,作DH⊥y轴于H,
则CH=DH=1,
∴∠HCD=∠HDC=45°,
∵OB=OC,

∴∠OCB=∠OBC=45°,
∴∠DCB=90°,
∴cot∠DBC=
| BC |
| DC |
3
| ||
|
(3)-x2+2x+3=0,
解得,x1=-1,x2=3,
∴点A的坐标为:(-1,0),
∴
| OA |
| OC |
| 1 |
| 3 |
| DC |
| BC |
| 1 |
| 3 |
∴
| OA |
| OC |
| DC |
| BC |
∴Rt△AOC∽Rt△DCB,
∴∠ACO=∠DBC,
∵∠ACB=∠ACO+45°=∠DBC+∠E,
∴∠E=45°,
∵△EBM和△ABC相似,∠E=∠ABC=45°,
∴∠ACB=∠BME,
∴BM=BC,
设直线CA的解析式为:y=kx+b,
则
|
解得,
|
则直线CA的解析式为:y=3x+3,
设点M的坐标为(x,3x+3),
则(x-3)2+(3x+3)2=18,
解得,x1=0(舍去),x2=-
| 6 |
| 5 |
x2=-
| 6 |
| 5 |
| 3 |
| 5 |
∴点M的坐标为(-
| 6 |
| 5 |
|
作业帮用户
2017-11-13

 |
看了 如图,已知抛物线y=-x2+...的网友还看了以下:
解方程组时舍多余解的问题方程组x2+y2+x+y=18x2+xy+y2=19我算出来8组解,然后带 2020-04-09 …
、若3x4+x3-4x2-17x+5除以x2+x+1的商式是ax2+bx+c,余式是dx+e,求( 2020-05-16 …
已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2,x1+x2=1-a,则()A.f 2020-05-17 …
设函数f(x)连续且恒大于零,F(t)=∫∫∫Ω(t)f(x2+y2+z2)dv∫∫D(t)f(x 2020-06-12 …
当x→0时,用o(x)表示比x高阶的无穷小,则下列式子中错误的是()A.x•o(x2)=o(x3) 2020-06-14 …
当x→0时,用o(x)表示比x高阶的无穷小,则下列式子中错误的是()A.xo(x2)=o(x3)B 2020-06-18 …
下列集合中,恰有2个元素的集合是()A.{x2-x=0}B.{x|x2-x=0}C.{x|y=x2 2020-06-27 …
函数f(x)=xln(1+x)带皮亚诺型余项的麦克劳林公式为x2−x32+x43−…+(−1)n− 2020-07-11 …
函数f(x)在(a,b)和(c,d)都是增函数,若x1∈(a,b),x2∈(c,d),且x1<x2 2020-07-13 …
待定系数法因式分解原式能分解成什么形式看两个例子:例1:x4-2x3-27x2-44x+7用待定系 2020-07-17 …
 扫描下载二维码
扫描下载二维码