早教吧作业答案频道 -->数学-->
如图,椭圆E:x2a2+y2b2=1(a>b>0)经过点A(0,-1),且离心率为22.(1)求a的值;(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的
题目详情
如图,椭圆E:
+
=1(a>b>0)经过点A(0,-1),且离心率为
.
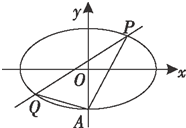
(1)求a的值;
(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |

(1)求a的值;
(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同的两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.
▼优质解答
答案和解析
(1) ∵椭圆E:
+
=1(a>b>0)经过点A(0,-1),且离心率为
,
∴b=1,
=
,
∴c=1,a=
.
(2)证明:由题设知,直线PQ的方程为y=k(x-1)+1(k≠2),
代入
+y2=1,得(1+2k2)x2-4k(k-1)x+2k(k-2)=0.
由已知△>0,
设P(x1,y1),Q(x2,y2),x1x2≠0,
则x1+x2=
,x1x2=
从而直线AP,AQ的斜率之和
kAP+kAQ=
+
=
+
=2k+(2-k)
=2k+(2-k)
=2k-2(k-1)=2.
所以直线AP、AQ斜率之和为定值2.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴b=1,
| c |
| a |
| ||
| 2 |
∴c=1,a=
| 2 |
(2)证明:由题设知,直线PQ的方程为y=k(x-1)+1(k≠2),
代入
| x2 |
| 2 |
由已知△>0,
设P(x1,y1),Q(x2,y2),x1x2≠0,
则x1+x2=
| 4k(k-1) |
| 1+2k2 |
| 2k(k-2) |
| 1+2k2 |
从而直线AP,AQ的斜率之和
kAP+kAQ=
| y1+1 |
| x1 |
| y2+1 |
| x2 |
| kx1+2-k |
| x1 |
| kx2+2-k |
| x2 |
=2k+(2-k)
| x1+x2 |
| x1x2 |
=2k+(2-k)
| 4k(k-1) |
| 2k(k-2) |
所以直线AP、AQ斜率之和为定值2.
看了 如图,椭圆E:x2a2+y2...的网友还看了以下:
若1/2+x+y=1(x>0,y>0),且1/x+a/y≥8恒成立,则正实数a的最小值为?求详解 2020-06-02 …
三点共线定理:若OC=λOA+μOB,且λ+μ=1,则A、B、C三点共线,这个λ+μ=1是如何推论 2020-06-23 …
已知a的平方加2a减1等于0,b的四次方减2b的平方减1等于0,且1减a乘b的平方不等于0,求a分 2020-07-08 …
若a>0,b>0,且1/a+1/b=根号ab(1)a^3+b^3最小值(2)是否存在a,若a>0, 2020-07-10 …
已知ab都是负实数,且1/a+1/b--1/a-b=0,那么b/a的值是多少?详细解答过程 2020-07-13 …
在三角形ABC中A.B.C对边a.b.c且1加A的正切除以B的正切的商等于2c除以b求角A 2020-07-30 …
设集合A={x|x²-3x+2=0},B={x|x²+2(a+1)x+(a²-5)=0},A∪B= 2020-08-01 …
已知a,b,c互不相等,且1/(x+a)+1/(y+a)+1/(z+a)=1/a,1/(x+b)+1 2020-11-08 …
有四个自然数1、a、b、c,满足a+b+c=2001,且1<a<b<c,这四个小自然数两两求和可得到 2020-11-18 …
某有机化合物A,含碳85.7%,含氧14.3%,具有与A相同化学式的链状同分异构体只有A、B、C三种 2020-11-20 …